Умножение и деление рациональных чисел. Умножение рациональных чисел. Является ли данное число рациональным

± d m … d 1 d 0 , d − 1 d − 2 … {\displaystyle \pm d_{m}\ldots d_{1}d_{0}{,}d_{-1}d_{-2}\ldots } ± {\displaystyle \pm } — знак дроби : либо + {\displaystyle +} , либо − {\displaystyle -} , , {\displaystyle ,} — десятичная запятая , служащая между целой и дробной частью числа () , d k {\displaystyle d_{k}} — . Причём последовательность цифр до запятой (слева от неё) конечна (как минимум одна цифра), а после запятой (справа от неё) — может быть как конечной (в частности, цифры после запятой могут вообще отсутствовать), так и бесконечной.

Значением десятичной дроби ± d m … d 1 d 0 , d − 1 d − 2 … {\displaystyle \pm d_{m}\ldots d_{1}d_{0},d_{-1}d_{-2}\ldots } является действительное число

± (d m ⋅ 10 m + … + d 1 ⋅ 10 1 + d 0 ⋅ 10 0 + d − 1 ⋅ 10 − 1 + d − 2 ⋅ 10 − 2 + …) , {\displaystyle \pm \left(d_{m}\cdot 10^{m}+\ldots +d_{1}\cdot 10^{1}+d_{0}\cdot 10^{0}+d_{-1}\cdot 10^{-1}+d_{-2}\cdot 10^{-2}+\ldots \right),}

Это свойство было использовано дважды в алгоритме. В самом начале построения выбиралось целое , такое, что действительное число находится между a 0 {\displaystyle a_{0}} и следующим целым a 0 + 1 {\displaystyle a_{0}+1} :

a 0 ⩽ α < a 0 + 1 , a 0 ∈ Z {\displaystyle a_{0}\leqslant \alpha

Однако существование такого целого числа a 0 {\displaystyle a_{0}} надо ещё доказать: нельзя исключать, например, возможность, когда, каково бы ни было целое n {\displaystyle n} , всегда имеет место неравенство n ⩽ α {\displaystyle n\leqslant \alpha } . Если бы этот случай имел место, то, очевидно, нужного числа a 0 {\displaystyle a_{0}} не нашлось бы.

Эта возможность как раз исключается аксиомой Архимеда, согласно которой каково бы ни было число α {\displaystyle \alpha } , всегда найдётся целое n {\displaystyle n} такое, что n > α {\displaystyle n>\alpha } . Теперь среди чисел k = 1 , … , n {\displaystyle k=1,\ldots ,n} возьмём наименьшее, обладающее свойством k > α {\displaystyle k>\alpha } . Тогда

k − 1 ⩽ α < k {\displaystyle k-1\leqslant \alpha

Искомое число найдено: a 0 = k − 1 {\displaystyle a_{0}=k-1} .

Второй раз аксиома Архимеда неявно использовалась при доказательстве стремления к нулю длин отрезков последовательности I 0 , I 1 , I 2 , … {\displaystyle I_{0},I_{1},I_{2},\ldots } :

lim n → ∞ 10 − n = 0 {\displaystyle \lim _{n\to \infty }10^{-n}=0}

Строгое доказательство данного предложения опирается на аксиому Архимеда. Докажем эквивалентное соотношение

В соответствии с аксиомой Архимеда, каково бы ни было действительное число E > 0 {\displaystyle E>0} , последовательность натуральных чисел 1 , 2 , … {\displaystyle 1,2,\ldots } превзойдёт его, начиная с некоторого номера. А поскольку для всякого n {\displaystyle n} имеет место неравенство

10 n > n {\displaystyle 10^{n}>n}

то последовательность 10 n {\displaystyle 10^{n}} также превзойдёт E {\displaystyle E} , начиная с того же номера. В соответствии с определением числовой последовательности, это означает, что lim n → ∞ 10 n = ∞ {\displaystyle \lim _{n\to \infty }10^{n}=\infty } .

Неоднозначность представления в виде десятичной дроби

С помощью приведённого алгоритма мы можем для любого действительного числа α {\displaystyle \alpha } построить десятичную дробь, представляющую данное число. Однако может случиться, что это же самое число α {\displaystyle \alpha } может быть представлено в виде десятичной дроби и другим образом.

Неединственность представления чисел в виде десятичных дробей уже следует из того тривиального факта, что, приписывая конечной дроби справа после запятой нули, мы будем получать формально различные десятичные дроби, представляющие одно и то же число.

Рассмотрим например, десятичную дробь

0 , 99 … {\displaystyle 0{,}99\ldots }

Согласно определению, эта дробь является представлением числа 0 + 9 / 10 + 9 / 100 + … = 1 {\displaystyle 0+9/10+9/100+\ldots =1} . Вместе с тем, это число может быть также представлено в виде десятичной дроби 1 , 00 … {\displaystyle 1{,}00\ldots } .

Этот пример можно обобщить. Можно показать, что дроби

± a 0 , a 1 … a n − 1 a n 999 … {\displaystyle \pm a_{0}{,}a_{1}\ldots a_{n-1}a_{n}999\ldots } ± a 0 , a 1 … a n − 1 (a n + 1) 000 {\displaystyle \pm a_{0}{,}a_{1}\ldots a_{n-1}(a_{n}+1)000}

где a n ≠ 9 {\displaystyle a_{n}\neq 9} , представляют одно и то же действительное число.

Оказывается, этим общим примером исчерпываются все случаи неоднозначности представления действительных чисел в виде десятичных дробей. При этом мы, конечно, не рассматриваем тривиальные случаи дробей, полученные приписыванием нулей в конец друг другу, а также пару дробей и .

Эти результаты можно суммировать в следующей теореме.

Теорема. Всякое действительное число α {\displaystyle \alpha } , не представимое в виде p / 10 s {\displaystyle p/10^{s}} , где p {\displaystyle p} — целое, s {\displaystyle s} — целое неотрицательное, допускает единственное представление в виде десятичной дроби; при этом эта дробь является бесконечной.

Всякое действительное число вида α = p / 10 s {\displaystyle \alpha =p/10^{s}} может быть представлено в виде десятичной дроби более чем одним способом. Если α ≠ 0 {\displaystyle \alpha \neq 0} , то оно может быть представлено как в виде конечной десятичной дроби, а также бесконечной дроби, полученной приписыванием нулей в конец после запятой, так и в виде бесконечной дроби, оканчивающейся на . Число α = 0 {\displaystyle \alpha =0} может быть представлено дробями вида + 0 , 00 … {\displaystyle +0{,}00\ldots } , а также дробями вида − 0 , 00 … {\displaystyle -0{,}00\ldots } .

Замечание. Бесконечные дроби, оканчивающиеся на 999 … {\displaystyle 999\ldots } , получаются, если в приведённом выше алгоритме всегда выбирать левый отрезок вместо правого .

Лишние нули и погрешность

Следует отметить, что, с точки зрения , запись десятичной дроби с нулями в конце не совсем тождественна записи без этих нулей.

Принято считать, что, если погрешность не указана, то десятичной дроби равна плюс-минус половине [ ] единицы последнего написанного разряда. Например, запись «3,7» означает, что абсолютная погрешность равна ±0,05. А в записи «3,700» абсолютная погрешность равна ±0,0005. Другие примеры:

«25» — абсолютная погрешность равна ±0,5 (также, такая запись может означать точное значение 25: например, 25 штук);
«25,0» — абсолютная погрешность равна ±0,05;
«25,00» — абсолютная погрешность равна ±0,005.

Периодические десятичные дроби

Бесконечная десятичная дробь называется периодической , если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр. Другими словами, периодическая дробь — десятичная дробь, имеющая вид

± a 0 , a 1 … a m b 1 … b l ⏟ b 1 … b l ⏟ … {\displaystyle \pm a_{0},a_{1}\ldots a_{m}\underbrace {b_{1}\ldots b_{l}} \underbrace {b_{1}\ldots b_{l}} \ldots }

Такую дробь принято кратко записывать в виде

± a 0 , a 1 … a m (b 1 … b l) {\displaystyle \pm a_{0},a_{1}\ldots a_{m}(b_{1}\ldots b_{l})}

Повторяющаяся группа цифр b 1 … b l {\displaystyle b_{1}\ldots b_{l}} называется периодом дроби, количество цифр в этой группе — длиной периода.

Если в периодической дроби период следует сразу после запятой, то дробь называется чистой периодической . Если же между запятой и первым периодом имеются цифры, дробь называется смешанной периодической , а группа цифр после запятой до первого знака периода — предпериодом дроби. Например, дробь 1 , (23) = 1,232 3 … {\displaystyle 1{,}(23)=1{,}2323\ldots } является чистой периодической, а дробь 0 , 1 (23) = 0,123 23 … {\displaystyle 0{,}1(23)=0{,}12323\ldots } — смешанной периодической.

Основное свойство периодических дробей, благодаря которому их выделяют из всей совокупности десятичных дробей, заключается в том, что периодические дроби и только они представляют . Точнее, имеет место следующее предложение.

Теорема. Всякая бесконечная периодическая десятичная дробь представляет рациональное число. Обратно, если рациональное число раскладывается в бесконечную десятичную дробь, то эта дробь является периодической.

Можно показать, что чисто периодические дроби соответствуют рациональным числам, в записи которых в виде несократимой дроби p / q {\displaystyle p/q} знаменатель q {\displaystyle q} не имеет

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели :

Познакомить с определением рациональных чисел и с логической схемой развития понятия числа.
Усвоить понятия:

конечная десятичная дробь;
бесконечная десятичная дробь;
периодическая бесконечная десятичная дробь.

Научить определять по виду обыкновенной дроби, какой десятичной дробью (конечной или бесконечной) она является.

Задачи:

Развивать умения составлять алгоритм действий и действовать по алгоритму.
Развивать умения анализировать полученные результаты, делать выводы и ставить новые вопросы.
Развивать умение использовать сформулированные правила при решении задач.
Развивать умения составлять и читать схемы.

Тип урока: изучение нового материала.

Метод: проблемно-исследовательский.

Форма: групповая.

Ход урока

Первая часть урока.

Цель первой части урока (теоретическая): выяснить и усвоить, какие числа называются и являются рациональными и есть ли числа, какие таковыми не являются.

1. В начале урока коротко повторить определения натуральных, дробных, целых чисел.

2. Объявляется тема урока: Рациональные числа. Обыкновенные и десятичные дроби. (Слайд 2). Формулируется цель первой части урока.

3. Формулируется определение рациональных чисел: Рациональным называют число, которое можно записать в виде отношения a/n , где a – целое число, а n – натуральное число. (Слайд 3). Рассматриваем примеры (Слайд 4).

4. Естественно возникает вопрос, какие же из известных нам чисел являются рациональными ? В ходе беседы на экране составляется логическая схема развития понятия числа (Рисунок 1 и Слайд 5). Приводим примеры и доказываем, что каждое из известных нам чисел является рациональным.

Рис. 1

5. Подробнее останавливаемся на десятичных дробях. Вспоминаем правило перевода десятичной дроби в обыкновенную (Слайд 6) и выполняем устно упражнение по переводу десятичной дроби в обыкновенную (Слайды 7–12).

(Устно) Переведите десятичную дробь в обыкновенную: 0,7; 0,75; 0,2; 0,16; 0,125; 0,375.

Дробь высвечивается на экране, дети поднимают карточку с верным ответом. Комплект карточек подготовлен заранее (Приложение 1) и лежит на столе у каждой группы; на карточках следующие числа 7/10, 75/100, 15/20, 3/4, 2/10, 1/5, 8/50, 4/25, 25/200, 1/8, 3/8, 5/8. Ответы комментируем, при необходимости выполняем пошаговую проверку (Слайды 7–12).

6. Приходим к выводу , что если десятичная дробь «получена» из обыкновенной, то эта десятичная дробь является рациональным числом.

Формулируется проблема: какими могут быть десятичные дроби и все ли десятичные дроби являются рациональными числами.

7. Для решения поставленных вопросов группы выполняют задание № 1 (Слайды 13–14) , (Приложение 2).

Задание № 1.1 (для группы 1)

Представьте обыкновенные дроби 1/4, 1/3, 1/6 в виде десятичных дробей.

Задание № 1.2 (для группы 2)

Представьте обыкновенные дроби 2/5, 4/11, 7/15 в виде десятичных дробей.

Проанализируйте полученные результаты.

Задание № 1.3 (для группы 3)

Представьте обыкновенные дроби 3/25, 1/37, 9/44 в виде десятичных дробей.

Проанализируйте полученные результаты.

Проанализировав результаты (Слайд 15) , а при необходимости, проверив вычисления (Слайды 16–18) , приходим к выводу, что десятичные дроби бывают а) конечные; б) бесконечные. А бесконечные обладают некоторым свойством: начиная с какого-то десятичного знака, один или несколько десятичных знаков повторяются. За это свойство такие бесконечные десятичные дроби назвали периодическими.

По ходу беседы на доске составляется схема. Таблички с надписями заготовлены заранее (Приложение 3) и крепятся магнитами к доске, а стрелочки можно нарисовать мелом.

Рис. 2

Дети делают вывод , что конечные десятичные дроби и бесконечные периодические десятичные дроби являются рациональными числами. Однако, учитель комментирует, что на данном этапе знаний этот вывод только предположение и, что требуется еще доказать, что любая периодическая десятичная дробь может быть представлена в виде обыкновенной, а значит, является рациональным числом, и мы докажем это позже, в 9 классе. А пока будем пользоваться этим положением как фактом.

8. Далее детям предлагается проанализировать составленную схему и подумать, могут ли быть еще какими-нибудь десятичные дроби (или можно предложить придумать такую десятичную дробь, которая не будет являться ни конечной, ни бесконечной периодической). Приходим к выводу, что существуют еще бесконечные непериодические дроби. Приводим примеры таких дробей (0,01001000100001…; 0,12123123412345123456… и т.п.), и говорим о том, что они не будут являться рациональными числами (и опять-таки это наше предположение, которое мы сможем доказать, но только позднее, а пока будем пользоваться только как фактом).

Рис. 3

Вторая часть урока.

Цель второй части урока (практическая): выяснить, как, по виду обыкновенной дроби понять, можно ли представить ее в виде конечной десятичной дроби, или получится бесконечная дробь.

9. Формулируем проблему: как по виду обыкновенной дроби понять, можно ли представить ее в виде конечной десятичной дроби, или получится бесконечная дробь.

Для решения этой проблемы выполним задания. Каждое из заданий № 2-4 выполняется по группам. После выполнения каждого задания обсуждаются результаты. Каждая группа формулирует свои выводы.

10. Задание №2 (Слайд 20, Приложение 2)

1/20, 1/25, 4/50, 3/125, 5/8, 17/100.

Разложите знаменатели данных дробей на множители.

Анализируем результаты (Слайд 20) (Слайд 21)

11. Задание №3 (Слайд 22, Приложение 2)

Переведите обыкновенные дроби в десятичные и ответьте на вопросы.

1/30, 3/110, 7/9, 8/55, 5/111, 7/82.

Разложите знаменатели данных дробей на множители
Каким общим свойством обладают знаменатели данных дробей?

Анализируем результаты (Слайд 23) , при необходимости проверив вычисления (Слайды 24–27) . Каждая группа сообщает о своих наблюдениях и делает предположительные выводы.

12. Задание №4 (Слайд 28 , Приложение 2)

Проанализируйте результаты предыдущих трех заданий и ответьте на вопросы:

Какие десятичные дроби «получаются» из обыкновенных дробей?
При каком условии обыкновенную дробь можно представить в виде конечной десятичной дроби?
При каком условии обыкновенную дробь можно представить в виде бесконечной периодической десятичной дроби?

Обсудив выступление представителя каждой группы по результатам задания № 4, переходим к выводам.

13. Выводы (Схема 2, Слайды 29–31 ):

Десятичные дроби бывают конечные и бесконечные.
Конечную десятичную дробь всегда можно представить в виде обыкновенной дроби и одна является рациональным числом.
Бесконечную периодическую десятичную дробь можно представить в виде обыкновенной дроби – это рациональное число.
Любую обыкновенную дробь можно представить в виде десятичной дроби конечной или бесконечной периодической.
Конечная десятичная дробь получится, если в разложении знаменателя соответствующей обыкновенной несократимой дроби нет других простых множителей кроме 2 и 5 (Слайд 30).
Бесконечная периодическая десятичная дробь получится, если в разложении знаменателя соответствующей обыкновенной несократимой дроби присутствует любой другой простой множитель, кроме 2 и 5 (Слайд 31).

14. Применение правила (Слайды 32–33) :

Задание №5

Какие из обыкновенных дробей 1/2, 1/3, 7/15, 6/25, 5/16 можно представить в виде конечной десятичной дроби?
В каких дробях (обыкновенных или десятичных) «удобнее» выполнить вычисления: а) 3/8 + 0, 567; б) 2,378 – 3/14 ?
В каких дробях (обыкновенных или десятичных) вы запишите решение уравнения:
1. 3х = 8;
2. 5у = 12;
3. 16а = –7?

Проверяем задание и подводим итоги:

15. Подведение итогов и постановка новых вопросов. (Рисунок 4, Слайды 34–35 ). Теперь мы знаем, что положительные и отрицательные обыкновенные дроби могут быть представлены в виде конечных или периодических десятичных дробей. Значит, последние являются рациональными числами. А бесконечные непериодические десятичные дроби таковыми не являются. По всей видимости, они входят в область каких-то других, не известных вам пока, чисел (по секрету скажу, что они называются иррациональными). Эти иррациональные числа вместе с рациональными тоже составляют свою область чисел, объединенных своими свойствами (действительные числа). А если, к области действительных чисел «добавить» еще какие-то числа, то,… Но это предмет будущих ваших исследований.

Рис. 4

16. Заключение урока (Слайд 36)

Урок заканчиваем цитатой Л.Н. Толстого: «Знание только тогда знание, когда оно добыто усилием собственной мысли, а не памятью». В этом ключе даем оценку работы каждой группы.

Домашнее задание:

Прочитать пункт 37 учебника. Какие вопросы, изложенные в тексте, мы не обсудили на уроке?
Придумать пять обыкновенных дробей, из которых «получаются» конечные десятичные дроби и пять обыкновенных дробей, из которых «получаются» бесконечные десятичные дроби (Приложение 4) и перевести эти дроби в десятичные.

Литература:

Шварцбурд С.И., Виленкин Н.Я., Жохов В.И., Чесноков А.С. Математика 6, Мнемозина, 2006.
Мордкович А.Г. Алгебра. 8 класс: Учебник для классов с углубленным изучением математики, Мнемозина, 2004.

Как известно, множество рациональных чисел (Q) включает в себя множества целых чисел (Z), которое в свою очередь включает множество натуральных чисел (N). Помимо целых чисел в рациональные числа входят дроби.

Почему же тогда все множество рациональных чисел рассматривают иногда как бесконечные десятичные периодические дроби? Ведь кроме дробей, они включают и целые числа, а также непериодические дроби.

Дело в том, что все целые числа, а также любую дробь можно представить в виде бесконечной периодической десятичной дроби. То есть для всех рациональных чисел можно использовать одинаковый способ записи.

Как представляется бесконечная периодическая десятичная дробь? В ней повторяющуюся группу цифр после запятой берут в скобки. Например, 1,56(12) - это дробь, у которой повторяется группа цифр 12, т. е. дробь имеет значение 1,561212121212... и так без конца. Повторяющаяся группа цифр называется периодом.

Однако в подобном виде мы можем представить любое число, если будем считать его периодом цифру 0, которая также повторяется без конца. Например, число 2 - это то же самое, что 2,00000.... Следовательно, его можно записать в виде бесконечной периодической дроби, т. е. 2,(0).

То же самое можно сделать и с любой конечной дробью. Например:

0,125 = 0,1250000... = 0,125(0)

Однако на практике не используют преобразование конечной дроби в бесконечную периодическую. Поэтому разделяют конечные дроби и бесконечные периодические. Таким образом, правильнее говорить, что к рациональным числам принадлежат

все целые числа,
конечные дроби,
бесконечные периодические дроби.

При этом просто помнят, что целые числа и конечные дроби представимы в теории в виде бесконечных периодических дробей.

С другой стороны, понятия конечной и бесконечной дроби употребимы к десятичным дробям. Если говорить об обыкновенных дробях, то как конечную, так и бесконечную десятичную дробь можно однозначно представить в виде обыкновенной дроби. Значит, с точки зрения обыкновенных дробей, периодические и конечные дроби - это одно и то же. Кроме того, целые числа также могут быть представлены в виде обыкновенной дроби, если представить, что мы делим это число на 1.

Как представить десятичную бесконечную периодическую дробь в виде обыкновенной? Чаще используют примерно такой алгоритм:

Приводят дробь к виду, чтобы после запятой оказался только период.
Умножают бесконечную периодическую дробь на 10 или 100 или … так, чтобы запятая передвинулась вправо на один период (т. е. один период оказался в целой части).
Приравнивают исходную дробь (a) переменной x, а полученную путем умножения на число N дробь (b) - к Nx.
Из Nx вычитают x. Из b вычитаю a. Т. е. составляют уравнение Nx – x = b – a.
При решении уравнения получается обыкновенная дробь.

Пример перевода бесконечной периодической десятичной дроби в обыкновенную дробь:
x = 1,13333...
10x = 11,3333...
10x * 10 = 11,33333... * 10
100x = 113,3333...
100x – 10x = 113,3333... – 11,3333...
90x = 102
x =

Понятия числа являются первичным и основным в математике. Это понятие прошло длительный путь исторического развития. Множество натуральных чисел

появилось в связи со счетом предметов. Затем под влиянием потребностей практики и развития самой математики были введены целые числа

и рациональные числа

Где .

Для однозначности записи рационального числа будем считать, что дробь не сократима, если не будет делаться оговорки на этот счет.

Введение рациональных чисел, однако, полностью не решило важной практической задачи об измерении отрезков. Ведь существует отрезок, длина которого не является рациональным числом. Примером может служить диагональ квадрата, сторона которого равна единице.

В связи с этим возникла необходимость введения, кроме рациональных чисел, и других чисел – иррациональных. Произвольные числа – рациональные или иррациональные - называются действительными или вещественными. Множество действительных чисел обозначают через . Существуют различные способы введения (определения) действительных чисел. Мы остановимся на способе представления их в виде бесконечных десятичных дробей

. (1)

Здесь - целое неотрицательное число, при - десятичные цифры. Таким образом, может принимать только одно из значений . Знак часто в этих записях опускают.

Чтобы представить не равное нулю рациональное число в виде десятичной дроби, производим процесс деления на по известному способу, которому нас учили в школе:

(2)

Заметим, что если этот способ применить к другой записи дроби , то получим тот же результат.

Полагаем

(3)

и правую часть (3) называем десятичным разложением числа .

Если знаменатель дроби имеет вид , где , - целые неотрицательные числа, то процесс (2) заканчивается после конечного числа шагов и получается конечная десятичная дробь

. (4)

Конечную десятичную дробь мы будем записывать также в виде бесконечной дроби:

Но пользуются также и другой записью:

хотя она не возникает из процесса (2).

Итак, имеют место равенства

Дроби и могут служить примерами периодических дробей. Первая из них после цифры имеет период 0, а вторая после цифры имеет период 9.

Пусть теперь знаменатель несократимой дроби не имеет вид . Тогда процесс (2) бесконечный – на любом шаге возникает положительный остаток. Каждый остаток меньше , и потому (после того, как цифры числа снесены) уже среди первых остатков, по крайней мере, два, равные между собой. Но, как только возникает остаток, который уже был прежде, процесс становится повторяющимся – периодическим. Поэтому, десятичное разложение произвольного рационального числа имеет вид

(6)

Разложения (5) и (5´) можно рассматривать как частные случаи (6).

(7)

Разложение вида (6) называется бесконечной десятичной периодической дробью.

Итак, каждое не равное нулю рациональное число можно разложить с помощью процесса (2), а в случае (4) и процесса (5) – в бесконечную периодическую дробь с периодом, отличным от 9. При этом можно доказать, что разным рациональным числам соответствуют разные бесконечные десятичные разложения. Но и обратно: любая бесконечная периодическая дробь (6), с периодом, отличным от 9, порождается при помощи указанных процессов (2), (5) некоторым рациональным числом, которое вычисляется по формуле

Здесь мы позволили себе через и обозначить целое число, записанное соответственно цифрами и .

Например,

Кроме периодических десятичных дробей, существуют непериодические, например ; .

Вот еще пример: если извлекать корень квадратный из 2 по известному правилу, то получим определенную бесконечную непериодическую десятичную дробь . Она определена в том смысле, что любому натуральному числу соответствует определенная цифра , стоящая на -м месте после запятой и однозначно вычисляемая согласно правилу извлечения квадратного корня.

Математический анализ дает много путей вычисления числа с любой наперед заданной точностью. Это приводит к вполне определенному бесконечному десятичному разложению , которое, как оказывается, не является смешенной периодической десятичной дробью.

Дадим теперь определение иррационального числа, пока чисто формальное. Иррациональным числом называется произвольная бесконечная непериодическая дробь

(8)

где - целое неотрицательное число, а - цифры, знак же равенства «=» выражает, что мы обозначили правую часть (8) через . Впрочем, удобно говорить, что правая часть (8) есть десятичное разложение числа .

Рациональные и иррациональные числа называются действительными (или вещественными) числами.

Из сказанного следует, что всякое не равное нулю действительное число может быть записано в виде бесконечной десятичной дроби (8). Если оно рациональное, то его десятичное разложение есть бесконечная периодическая десятичная дробь. В противном случае, согласно нашему определению, выражение (8) само определяет иррациональное число.

Не равная нулю десятичная дробь может быть конечной, но она не определяет нового рационального числа: в силу соглашений, выраженных равенствами (5), (5´), она может быть заменена указанными в этих равенствах бесконечными периодическими дробями.

Число , где не все равны нулю, положительно или отрицательно в зависимости от того, будет ли в (8) фигурировать или ; при этом, как обычно, будем опускать.

Число 0 тоже может быть записано бесконечной десятичной дробью одного из следующих видов:

Действительные числа определены пока формально, надо еще определить арифметические операции над ними, ввести понятие и проверить, что эти операции и понятие согласуются с уже имеющимися соответствующими операциями и понятием для рациональных чисел, а также удовлетворяют свойствам, которые мы предъявляем к числам.

В данном уроке рассматривается умножение и деление рациональных чисел.

Содержание урока

Умножение рациональных чисел

Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь

Также, необходимо знать основные законы умножения, такие как: переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и умножение на ноль.

Пример 1. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.

Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками

Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.

Короткое решение выглядит следующим образом:

Пример 2. Найти значение выражения

Пример 3. Найти значение выражения

Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

Решение для данного примера можно записать покороче:

Пример 4. Найти значение выражения

Решение для данного примера можно записать покороче:

Пример 5. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

Короткое решение будет выглядеть значительно проще:

Пример 6. Найти значение выражения

Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть

Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение

Решение для данного примера можно записать покороче

Пример 7. Найти значение выражения

Сначала в ответе получилась неправильная дробь , но мы выделили в ней целую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.

Решение для данного примера можно записать покороче:

Пример 8. Найти значение выражения

Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.

Ответ: значение выражения равно −2.

Пример 9. Найти значение выражения:

Переведём смешанные числа в неправильные дроби:

Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение

Пример 10. Найти значение выражения

Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.

Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение

Третье действие:

Четвёртое действие:

Ответ: значение выражения равно

Пример 11. Найти значение выражения

Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.

В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:

Пример 12. Найти значение выражения

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Пример 13. Найти значение выражения

Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .

Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.

Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те параметры, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:

Третье действие:

Ответ: значение выражения равно

Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:

Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.

Пример 14. Найти значение выражения −4,2 × 3,2

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось .

Пример 15. Найти значение выражения −0,15 × 4

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь .

Пример 16. Найти значение выражения −4,2 × (−7,5)

Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс

Деление рациональных чисел

Правила деления целых чисел справедливы и для рациональных чисел. Иными словами, чтобы уметь делить рациональные числа, нужно уметь

В остальном же применяются те же методы деления обыкновенных и десятичных дробей. Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.

А чтобы разделить десятичную дробь на другую десятичную дробь, нужно в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, затем выполнить деление, как на обычное число.

Пример 1. Найти значение выражения:

Это деление рациональных чисел с разными знаками. Чтобы вычислить такое выражение, нужно первую дробь умножить на дробь, обратную второй.

Итак, умножим первую дробь на дробь обратную второй.

Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули этих рациональных чисел и перед полученным ответом поставить минус.

Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение

Таким образом, значение выражения равно

Подробное решение выглядит следующим образом:

Короткое решение будет выглядеть так:

Пример 2. Найти значение выражения

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно первую дробь умножить на дробь, обратную второй.

Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Короткое решение будет выглядеть следующим образом:

Пример 3. Найти значение выражения

Это деление отрицательных рациональных чисел. Чтобы вычислить данное выражение, опять же нужно первую дробь умножить на дробь обратную второй.

Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Получили умножение отрицательных рациональных чисел. Как вычисляется подобное выражение мы уже знаем. Нужно перемножить модули рациональных чисел и перед полученным ответом поставить плюс.

Дорешаем этот пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение:

Пример 4. Найти значение выражения

Чтобы вычислить данное выражение, нужно первое число −3 умножить на дробь, обратную дроби .

Обратная для дроби это дробь . На неё и умножим первое число −3

Пример 6. Найти значение выражения

Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу 4.

Обратное для числа 4 это дробь . На неё и умножим первую дробь

Пример 5. Найти значение выражения

Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу −3

Обратное для числа −3 это дробь . На неё и умножим первую дробь:

Пример 6. Найти значение выражение −14,4: 1,8

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус

Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае, чтобы сделать это правильно, потребовалось суметь .

Если нет желания возиться с десятичными дробями (а это бывает часто), то эти , затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.

Вычислим предыдущее выражение −14,4: 1,8 этим способом. Переведём десятичные дроби в смешанные числа:

Теперь переведём полученные смешанные числа в неправильные дроби:

Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:

Пример 7. Найти значение выражения

Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:

Многоэтажные дроби

Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:

В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:

В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной .

При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.

Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.

Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.

После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:

Пример 2.

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь

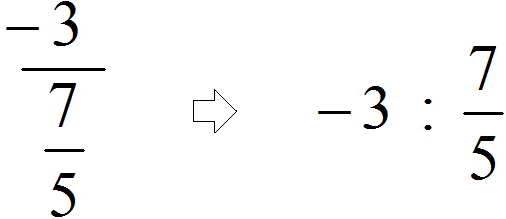
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .

Пример 3. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2

А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.

Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.

Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.

Реализуется этот метод следующим образом:

Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)

В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!

Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:

С первого на четвёртый. Со второго на третий.

В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.

Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.

Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж

В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь пользуясь новой схемой.

Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть

В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.

Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:

В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:

Использование переменных

Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.

Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.

Использование переменных оправдано, при работе с многоэтажными дробями. Например:

Найти значение выражения

Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.

Выражение, находящееся в числителе можно занести в переменную с любым названием, например:

Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A

А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B

Теперь наше изначальное выражение принимает вид . То есть, мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.

Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .

Найдём значение переменной A

Найдём значение переменной B

Теперь подставим в главное выражения вместо переменных A и B их значения:

Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:

Таким образом, значение выражения равно −1.

Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.

Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как

Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках