Спектральный состав периодической последовательности прямоугольных импульсов. Анализ спектра последовательности прямоугольных импульсов. Пример спектра периодической последовательности прямоугольных импульсов
Название образовательной организации:
Государственное бюджетное профессиональное образовательное учреждение «Ставропольский колледж связи имени Героя Советского Союза В.А. Петрова»
Год и место создания работы: 2016 год, цикловая комиссия естественных и общепрофессиональных дисциплин.
Методические указания к выполнению практической работы по дисциплине «Теория электросвязи»
«Расчет и построение спектра периодической последовательности прямоугольных импульсов»
для студентов 2 курса специальностей:
11.02.11 Сети связи и системы коммутации
11.02.09 Многоканальные телекоммуникационные системы
очной формы обучения
Цель работы: закрепить знания, полученные на теоретических занятиях, выработать навыки расчета спектра периодической последовательности прямоугольных импульсов.
Литература: П.А. Ушаков «Цепи и сигналы электросвязи». М.: Издательский центр «Академия», 2010, с.24-27.
1. Оснащение:
1.Персональный компьютер
2.Описание практической работы
2. Теоретический материал
2.1. Периодический сигнал произвольной формы может быть представлен в виде суммы гармонических колебаний с разными частотами, это называется спектральным разложение сигналом.
2.2 . Гармониками называются колебания, частоты которых в целое число раз больше частоты следования импульсов сигнала.
2.3. Мгновенное значение напряжения периодического сигнала производной формы может быть записано следующим образом:
Где постоянная составляющая, равная среднему значению сигнала за период;
Мгновенное значение синусоидального напряжения первой гармоники;
Частота гармоники, равная частоте следования импульсов;
Амплитуда первой гармоники;
Начальная фаза колебания первой гармоники;
Мгновенное значение синусоидального напряжения второй гармоники;
Частота второй гармоники;
Амплитуда второй гармоники;
Начальная фаза колебания второй гармоники;
Мгновенное значение синусоидального напряжения третий гармоники;
Частота третий гармоники;
Амплитуда третий гармоники;
Начальная фаза колебания третий гармоники;
2.4. Спектр сигнала - это совокупность гармонических составляющих с конкретными значениями частот, амплитуд и начальных фаз, образующих в сумме сигнала. На практике чаще всего используется диаграмма амплитуд

Если сигнал представлен собой периодическую последовательность прямоугольных импульсов, то постоянная составляющая равна
где Um - амплитуда напряжения ПППИ
s - скважность сигнала (S - T/t);
T - период следования импульсов;
t - длительность импульсов;
Амплитуды всех гармоник определяются выражением:
Umk = 2Um | sin kπ/s | / kπ
где k - номер гармоника;
2.5. Номера гармоника, амплитуды которых равны нулю
где n - любое целое число 1,2,3…..
Номер гармоники, амплитуда которой первый раз обращается в нуль, равен скважности ПППИ
2.6. Интервал между любыми соседними спектральными линиями равен частоте первой гармоники или частоте следования импульсов.
2.7 Огибающая амплитудного спектра сигнала (на рис. 1 показанная пунктирной линией)
выделяет группы спектральных линий называемых лепестками. Согласно рис. 1 каждый лепесток огибающей спектра содержит число линий, равное скважности сигнала.
3 . П орядок выполнения работы .
3.1. Получить вариант индивидуального задания, который соответствует номеру в списке журнала группы (см. приложение).
3.2. Ознакомиться с примером расчета (см. раздел 4)
4. Пример
4.1. Пусть период следования ПППИ Т=.1мкс, длительность импульсов t=0,25 мкс, амплитуда импульса =10В.
4.2. Расчет и построение временной диаграммы ПППИ.
4.2.1 . Для построения временной диаграммы ПППИ необходимо знать период следования импульсов Т, амплитуду и длительность импульсов t, которые известны из условия задачи.
4.2.2. Для построения временной диаграммы ПППИ необходимо выбрать масштабы по осям напряжений и времени. Масштабы должны соответствовать числам 1,2 и 4, умноженным на 10 n -(где n=0,1,2,3...). Ось времени должна занимать примерно 3/4 ширины листа и на ней следует разместить 2-3 периода сигнала. Вертикальная ось напряжений должна быть равна 5-10 см. При ширине листа 20 см длинна оси времени должна равна примерно 15 см. На 15-ти см удобно разместить 3 периода, при этом на каждый период будет приходиться L 1 =5см. Так как
Mt=T/Lt=1мкс/5см= 0,2 мкс/см
Полученный результат не противоречит выше указанным условиям. На оси напряжений удобно взять масштаб Мu=2В/см (см.рис.2).

4.3.Расчет и построение спектральной диаграммы.
4.3.1.Скважность ПППИ равна
![]()
4.3.2. Так как скважность S=4, то следует рассчитывать 3лепестка, т.к. 12 гармоник.
4.3.3.Частоты гармонических составляющих равны
Где к- номер гармоники, l- период ПППИ.
![]()
4.3.4. Амплитуды составляющих ПППИ равны
4.3.5. Математическая модель ПППИ напряжения
4.3.6.Выбор масштабов.
Ось частот располагается горизонтально и при ширине листа 20см должна иметь длину около 15 см. Так как на оси частот нужно показать самую высокую частоту 12 МГц удобно взять масштаб по этой оси Mf=1MГц/см.
Ось напряжений располагается вертикально и должна иметь длину 4-5 см. Так как из оси напряжений нужно показать самое большое напряжение
Удобно взять масштаб по этой оси M=1В/см.
4.3.7.Спектральная диаграмма показана на рис.3
Задание:
T=0.75мс; τ=0.15мс 21.T=24мкс; τ=8мкс
T=1.5 мкс; τ=0.25мкс 22. T=6.4мс; τ=1.6мс
T=2.45мс; τ=0.35мс 23. T=7мс; τ=1.4мс
T=13.5мкс; τ=4.5мкс 24. T=5.4мс; τ=0.9мс
T=0.26мс; τ=0.65мкс 25. T=17.5мкс; τ=2.5мкс
Т=0.9мс; τ=150мкс 26. T=1.4мкс; τ=0.35мкс
Т=0.165мс; τ=55мкс 27. T=5.4мкс; τ=1.8мкс
Т=0.3мс; τ=75мкс 28. T=2.1мс; τ=0.3мс
Т=42.5мкс; τ=8.5мкс 29. T=3.5мс; τ=7мс
Т=0.665мс; τ=95мкс 30. T=27мкс; τ=4.5мкс
Т=12.5мкс; τ=2.5мкс 31. T=4.2мкс; τ=0.7мкс
Т=38мкс; τ=9.5мкс 32.T=28мкс; τ=7мкс
Т=0.9мкс; τ=0.3мкс 33. T=0.3мс; τ=60мкс
Т=38.5мкс; τ=5.5мкс
Т=0.21мc; τ=35мс
Т=2.25мс; τ=0.45мс
Т=39мкс; τ=6.5мкс
Т=5.95мс; τ=0.85мс
Т=48мкс; τ=16мкс
СИГНАЛОВ
Рассмотрим несколько примеров периодических колебаний, часто используемых в различных радиотехнических устройствах.
1. ПРЯМОУГОЛЬНОЕ КОЛЕБАНИЕ (РИС. 2.3)
Подобное колебание, часто называемое меандром, находит особенно широкое применение в измерительной технике.
При выборе начала отсчета времени в соответствии с рис. 2.3, а функция является нечетной, а рис. 2.3, б - четной. Применяя формулы (2.24), находим для нечетной функции (рис. 2.3, а) при s(t)=e(t):

Рис. 2.3. Периодическое колебание прямоугольной формы (меандр)

Рис. 2.4. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье колебания, показанного на рис. 2.3
Учитывая, что , получаем
Начальные фазы в соответствии с (2.27) равны для всех гармоник.
Запишем ряд Фурье в тригонометрической форме

Спектр коэффициентов комплексного ряда Фурье показан на рис. 2.4, а, а тригонометрического ряда - на рис. 2.4, б (при ).
При отсчете времени от середины импульса (рис. 2.3, б) функция является четной относительно t и для нее
Графики 1-й гармоник и их суммы изображены на рис. 2.5, а. На рис. 2.5, б эта сумма дополнена 5-й гармоникой, а на рис. 2.5, в - 7-й.
С увеличением числа суммируемых гармоник сумма ряда приближается к функции всюду, кроме точек разрыва функции, где образуется выброс. При величина этого выброса равна , т. е. сумма ряда отличается от заданной функции на 18%. Этот дефект сходимости в математике получил название явления Гиббса.

Рис. 2.5. Суммирование 1-й и 3-й гармоник (а), 1, 3 и 5-й гармоник (б), 1, 3, 5 и 7-й гармоник (в) колебания, показанного на рис. 2.3

Рис. 2.6 Периодическое колебание пилообразной формы

Рис. 2.7. Сумма первых пяти гармоник колебания, показанного на рис. 2.6
Несмотря на то, что в рассматриваемом случае ряд Фурье не сходится к разлагаемой функции в точках ее разрыва, ряд сходится в среднем, поскольку при выбросы являются бесконечно узкими и не вносят никакого вклада в интеграл (2.13).
2. ПИЛООБРАЗНОЕ КОЛЕБАНИЕ (РИС. 2.6)
С подобными функциями часто приходится иметь дело в устройствах для развертки изображения в осциллографах. Так как эта функция является нечетной, ряд Фурье для нее содержит только синусоидальные члены. С помощью формул (2.24)-(2.31) нетрудно определить коэффициенты ряда Фурье. Опуская эти выкладки, напишем окончательное выражение для ряда

Как видим, амплитуды гармоник убывают по закону , где . На рис. 2.7 показан график суммы первых пяти гармоник (в увеличенном масштабе).
3. ПОСЛЕДОВАТЕЛЬНОСТЬ УНИПОЛЯРНЫХ ТРЕУГОЛЬНЫХ ИМПУЛЬСОВ (РИС. 2.8)
Ряд Фурье для этой функции имеет следующий вид:

Рис. 2.8. Сумма трех первых гармоник периодической функции

Рис. 2.9. Периодическая последовательность прямоугольных импульсов с большой скважностью
На рис. 2.8 изображена сумма первых трех членов этого ряда. В данном случае отметим более быстрое убывание амплитуд гармоник, чем в предыдущих примерах. Это объясняется отсутствием разрывов (скачков) в функции.
4. ПОСЛЕДОВАТЕЛЬНОСТЬ УНИПОЛЯРНЫХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ (РИС 2.9)
Применяя формулу (2.32), находим среднее значение (постоянную составляющую)

и коэффициент гармоники

2. Спектр периодической последовательности прямоугольных импульсов
Рассмотрим периодическую последовательность прямоугольных импульсов, изображенную на рис. 5. Данный сигнал характеризуется длительностью импульса, его амплитудой и периодом. По вертикальной оси откладывается напряжение.
Рис.5. Периодическая последовательность прямоугольных импульсов
Начало отсчета выберем в середине импульса. Тогда сигнал разлагается только по косинусам. Частоты гармоник равныn/T , где n - любое целое число. Амплитуды гармоник согласно (1.2.) будут равны :

так как V(t) =Е при , где - длительности импульса и V(t) =0 при , то

Эту формулу удобно записать в виде:
 (2.1.)
(2.1.)

Рис.6. Спектр периодической последовательности
прямоугольных импульсов.
При построении огибающей имеем ввиду, что - является
Осцилирующей функцией частоты, а знаменатель монотонно возрастает с ростом частоты. Поэтому получается квазиосцилирующая функция с постепенным убыванием. При частоте стремящейся к нулю, к нулю стремятся одновременно и числитель и знаменатель, их отношение стремится к единице (первый классический предел). Нулевые значения огибающей возникают в точках где т. е.
Где m – целое число (кроме m
Спектральное представление временных функций широко используется в теории связи. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используется различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательности прямоугольных и радиоимпульсов и т. д. Особо важную роль в теоретических исследованиях электрических цепей играют вычислительные сигналы в форме единичной функции и импульсной функции (функции Дирака). Определим спектры наиболее распространенных типовых сигналов.
11.1 Спектр последовательности прямоугольных импульсов
Пусть имеется периодическая последовательность импульсов прямоугольной формы периодом Т длительностью импульсов t и и амплитудой А. Аналитическое выражение функции , описывающей импульс на отрезке , имеет вид
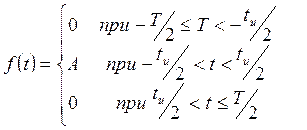 (11.1)
(11.1)
График периодической последовательности импульсов изображен на рисунке 11.1.

Рисунок 11.1
Данная функция является четной, так как ее график симметричен относительно оси ординат. Тогда коэффициенты Фурье это функции вычисляются по формулам (КФТ2), где .

Число представляет собой среднее значение функции за период и называется постоянной составляющей. Частоту называют основной, или первой гармоникой, а частоты k высшими гармониками, где k=2,3,4,…
Построим амплитудный спектр рассматриваемой последовательности прямоугольных импульсов. Так как функция периодическая, то ее амплитудный спектр является линейчатым. Обозначим через расстояние между любыми соседними гармониками. Очевидно, оно равно . Амплитуда k-ой гармоники согласно (11.2) имеет вид
 (11.3)
(11.3)
Найдем отношение между периодом Т и длительностью импульса , при котором амплитуда k-ой гармоники обращается в нуль.
А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6,36В, А 6 ≈10,5В, А 7 ≈6,36В, А 8 ≈0, А 9 ≈4,95В, А 10 ≈6,37В.
Полученный в результате расчета амплитудный спектр приведен на рисунке 11.2.

Рисунок 11.2
Такой спектр называют линейчатым или дискретным спектром.
Аналогично рассчитаны и построены спектры для q=8 и q=16. Они приведены на рисунках 11.3 и 11.4 соответственно.

Рисунок 11.3

Рисунок 11.4
Из рисунка видно, что чем больше скважность прямоугольных импульсов, тем меньше значение имеет амплитуда первой гармоники, но тем медленнее убывает спектр.
11.2 Спектр одиночного прямоугольного импульса
Рассмотрим Ф (11.1) для случая, когда Т→∞, то есть периодическая последовательность импульсов вырождается в одиночный прямоугольный импульс, длительностью t u .
Аналитическое выражение для этого импульса запишется в виде:
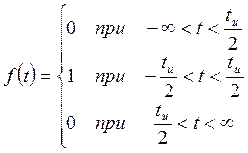
График этой функции изображен на рисунке 11.5.
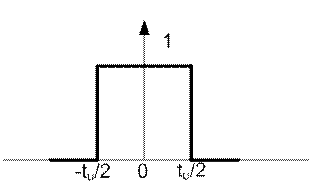
Рисунок 11.5
В этом случае частота первой гармоники и расстояние между гармониками становится равным 0, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга. Такой спектр называют сплошным. Отсюда следует важнейшее правило: периодические сигналы порождают дискретные спектры, а непериодические – сплошные (непрерывные).
Спектр прямоугольного одиночного импульса можно найти непосредственно из прямого преобразования Фурье (10.1)
В данном выражении
| |
функция sinc, как показано на рис. 2.6, достигает максимума (единицы) при у = 0и стремится к нулю при у ® ±¥, осциллируя с постепенно уменьшающейся амплитудой. Через нуль она проходит в точках у = ±1, ±2, …. На рис. 2.7, а как функция отношения п/Т 0 показан амплитудный спектр последовательности импульсов |с n |, а на рис. 2.7, б изображен фазовый спектр q n . Следует отметить, что положительные и отрицательные частоты двустороннего спектра - это полезный способ математического выражения спектра; очевидно, что в реальных условиях воспроизвести можно только положительные частоты.
Отношение
Идеальная периодическая последовательность импульсов включает все гармоники, кратные собственной частоте. В системах связи часто предполагается, что значительная часть мощности или энергии узкополосного сигнала приходится на частоты от нуля до первого нуля амплитудного спектра (рис. 2.7, а ). Таким образом, в качестве меры ширины полосы последовательности импульсов часто используется величина 1/T (где Т - длительность импульса). Отметим, что ширина полосы обратно пропорциональна длительности импульса; чем короче импульсы, тем более широкая полоса с ними связана. Отметим также, что расстояние между спектральными линиями Df = 1/Т 0 обратно пропорционально периоду импульсов; при увеличении периода линии располагаются ближе друг к другу.
Таблица 2.1. Фурье-образы
| x (t ) | X (f ) |
| d(t ) | |
| d(f ) | |
| cos 2 pf 0 t | /2 |
| sin 2 pf 0 t | /2 |
| d(t - t 0) | |
| d(f - f 0) | |
| , a >0 | |
 | |
| | |
| exp(-at )u (t ), a >0 | |
| rect(t / T ) | T sinc fT |
| W sinc Wt | rect (f / W ) |
 |
 sinc x
=
sinc x
=
Таблица 2.2 Свойства преобразования Фурье f )
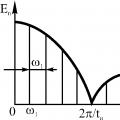 Анализ спектра последовательности прямоугольных импульсов
Анализ спектра последовательности прямоугольных импульсов «Тоска», анализ произведения Чехова, сочинение
«Тоска», анализ произведения Чехова, сочинение Ковалентные пи-связи и сигма-связи
Ковалентные пи-связи и сигма-связи