Расстояние между кластерами. Факультет экономики и управления. Между параллельными плоскостями
Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве. Например, если вы должны кластеризовать типы еды в кафе, то можете принять во внимание количество содержащихся в ней калорий, цену, субъективную оценку вкуса и т.д. Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если вы имеете двух- или трёхмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой). Однако алгоритм объединения не «заботится» о том, являются ли «предоставленные» для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений.
Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:
расстояние(x,y) = {? i (x i — y i) 2 } 1/2
Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.
Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (см. также замечания в предыдущем пункте):
расстояние(x,y) = ? i (x i — y i) 2
Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:
расстояние(x,y) = ? i |x i — y i |
Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:
расстояние(x,y) = Максимум|x i — y i |
Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния . Степенное расстояние вычисляется по формуле:
расстояние(x,y) = (? i |x i — y i | p) 1/r
где r и p — параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как «работает» эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра — r и p , равны двум, то это расстояние совпадает с расстоянием Евклида.
Процент несогласия. Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:
расстояние(x,y) = (Количество x i ?y i)/ i
Правила объединения или связи
На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос, как следует определить расстояния между кластерами? Другими словами, необходимо правило объединения или связи для двух кластеров. Здесь имеются различные возможности: например, вы можете связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи. Другими словами, вы используете «правило ближайшего соседа» для определения расстояния между кластерами; этот метод называется методом одиночной связи . Это правило строит «волокнистые» кластеры, т.е. кластеры, «сцепленные вместе» только отдельными элементами, случайно оказавшимися ближе остальных друг к другу. Как альтернативу вы можете использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется метод полной связи . Существует также множество других методов объединения кластеров, подобных тем, что были рассмотрены.
Одиночная связь (метод ближайшего соседа). Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными «цепочками».
Полная связь (метод наиболее удаленных соседей). В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. «наиболее удаленными соседями»). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных «рощ». Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.
Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных («цепочного» типа) кластеров. Отметим, что в своей книге Снит и Сокэлвводят аббревиатуру UPGMA метод невзвешенного попарного арифметического среднего
Взвешенное попарное среднее. Метод идентичен методу невзвешенного попарного среднего , за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров. В книге Снита и Сокэлавводится аббревиатура WPGMA для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего
Невзвешенный центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл используют аббревиатуру UPGMC для ссылки на этот метод, как на
Взвешенный центроидный метод (медиана). тот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т.е. числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. Снит и Сокэл использовали аббревиатуру WPGMC для ссылок на него, как на метод невзвешенного попарного центроидного усреднения
Метод Варда. Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Подробности можно найти в работе Варда В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.
До сих пор мы работали с объектами, все характеристики которых измерялись в одной из сильных шкал, и потому оценивать расстояние между объектами было несложно. Однако в реальных задачах часто встречаются таблицы со свойствами, измеренными в разных шкалах, в том числе в порядковых и номинальных. В этом случае возникает непростая проблема оценки меры расстояния, близости, похожести как между объектами (строками), так и между свойствами (столбцами).
Этой проблеме посвящены многие работы (см., например, ). Как правило, ищутся такие меры, которые удовлетворяли бы обычным аксиомам метрического пространства (непрерывности, симметричности и т. п.), были инвариантны к допустимым преобразованиям для данного типа шкалы и не зависели от состава изучаемых объектов. Итоги этих рассмотрений сводятся к тому, что меры, инвариантные к допустимым преобразованиям для многих шкал, можно указать, а мер, которые не зависели бы от состава выборки, не существует. Добавление к конечной выборке или изъятие из нее какого- нибудь объекта может изменить прежние порядковые номера объектов и (для шкал порядка) или нормировку (для более сильных шкал), что приводит к изменению расстояния между -м и -м объектами.
Какой же вывод нужно сделать из этих результатов? Не следует ли признать, что адекватных мер близости между объектами любой конечной выборки нет, а следовательно, нет и оснований верить результатам решения всех тех задач, в которых существенно используются меры близости или меры расстояния между объектами, т. е. задач таксономии, распознавания образов, корреляционного, регрессионного анализа и т. п.?
Не будем спешить соглашаться с таким пессимистическим заключением. Вспомним, что меняется не при всяком изменении состава выборки . Действительно, при нормировке сильных шкал по разности между самым большим и самым малым значением характеристики в таблице, т. е. по , мера будет сохраняться всегда, пока изменения состава объектов не коснутся объектов с или . Для любых шкал нормированная мера остается неизменной, если в таблице продублировать все объекты любое число раз. Если же встречаются другие ситуации, то это означает, что первоначальный состав выборки плохо отражал свойства генеральной совокупности.
Таким образом, указанные выше трудности отражают фундаментальную для всех естественнонаучных дисциплин проблему представительности выборки. Формальными методами эту проблему решить невозможно. Исследователь должен либо знать, что выборка включает полный набор изучаемых объектов, и тогда трудности, описанные выше, возникнуть не могут. Либо он должен верить в то, что выборка представляет лишь часть генеральной совокупности , но достаточно хорошо отражает ее закономерности, т. е. что выборка представительна. Тогда меры будут одинаковыми для объектов и независимо от того, рассматриваем ли мы их на фоне выборки или на фоне генеральной совокупности . Выводы (т. е. таксономия, решающие правила, регрессионные уравнения и т. д.), сделанные на основании такой выборки, будут сохраняться и на генеральной совокупности. Некоторые отклонения от идеальной представительности можно частично компенсировать применением процедур, повышающих устойчивость к случайным возмущениям. Например, нормировку делать не по крайним значениям характеристик, а по их дисперсии или медиане.
А если выборка непредставительна, то никакие формальные ухищрения, в том числе и гарантии инвариантности к допустимым преобразованиям шкал, не имеют смысла: из-за непредставительности индуктивные выводы для все равно будут ложными.
В итоге вопрос о том, верить или нет мере расстояния , сводится к вопросу о том, представительна выборка или нет. Эвристические способы получения некоторого представления о степени представительности выборки при решении задач распознавания образов обсуждались в § 10 главы 5. Если есть возможность, то малопредставительную выборку пополняют новыми объектами и тем самым увеличивают ее представительность. После того, как все такие возможности исчерпаны, вырабатывается оценка ожидаемой ошибки анализа и, если она устраивает пользователя, переходят к решению задачи анализа этих данных, полагаясь при этом на меры расстояния между объектами, вычисляемые по данным из таблицы .
Рассмотрим, какие меры расстояния можно использовать при обработке разнотипных шкал. Нам хотелось бы иметь меры , обладающие следующими очевидными свойствами:
а) непрерывности: мера должна быть непрерывной функцией своих аргументов;
б) симметричности: предполагая пространство значений аргументов
изотропным, потребуем, чтобы выполнялось соотношение ![]() ;
;
в) нормированности: мера должна меняться в пределах от нуля до единицы, причем , если ;
г) инвариантности: для преобразования , допустимого в шкале данного типа, ;
д) свойствам треугольника: для любых трех объектов справедливо, что ![]() .
.
Не для всех задач анализа данных нужны меры, которые удовлетворяли бы всем указанным выше требованиям. Часто достаточно, чтобы сохранялась информация о свойствах объектов лишь с точностью до порядка, так что требование г) можно было бы ослабить, а требование д) снять совсем. Однако мы попытаемся найти более универсальную меру, удовлетворяющую всем требованиям от а) до д). Не будем останавливаться на сильных шкалах (выше шкалы порядка). Для них свойствам а)-д) удовлетворяет, например, мера . Оговоримся лишь, что для частного случая, когда , неопределенное отношение 0/0 принимается равным нулю.
Рассмотрим шкалу порядка. Напомним, что при всех допустимых преобразованиях для этой шкалы отношения из набора между двумя числами , и должны сохраняться и для чисел и . Если мы построим матрицу размером (где - число объектов в выборке ), в которой для каждой пары объектов укажем их отношение в шкале порядка, то эта матрица не изменится при всех возможных преобразованиях группы . В -й строке этой матрицы представлена информация о том, в каких порядковых отношениях находится -й объект ко всем остальным объектам таблицы или какую порядковую роль играет он в этой таблице (матрице ролей). Естественно считать, что одинаковы два объекта, имеющие одинаковые порядковые отношения со всеми другими объектами. Различия в отношениях -го и -го объектов к некоторому -му объекту будем оценивать, анализируя содержание элементов на пересечении -го столбца с -й и -й строками. При этом будем считать, что

Суммарное различие между ролями объектов и во множестве получаем из равенства
![]()
Легко видеть, что если , то , и что для объектов и , имеющих максимально разные порядковые позиции, . Очевидно выполнение и других требований к .
Напомним, что данные,
измеренные в шкале порядка, можно без искажения содержания представить в шкале
«нормированных рангов»: первому по порядку присваивается число 1, второму -
число 2 и так до конца. Если встретятся объектов с
одинаковым порядковым номером (так называемые серии), то всем им присваивается
номер «среднего» для них места: ![]() , где - количество объектов, предшествовавших серии.
После такой канонизации расстояние находится
по правилу
, где - количество объектов, предшествовавших серии.
После такой канонизации расстояние находится
по правилу
В том, что эта мера равна мере, вычисленной выше по матрице ролей, легко убедиться на примере, приведенном в табл. 4. Здесь данные в шкале порядка имеют следующие значения: . Те же данные в нормированных рангах принимают значения: .
Таблица 4.Матрица ролей в шкале порядка
Перейдем теперь к шкале наименований. Допустимые преобразования для шкал этого типа всегда сохраняют отношения «равно» и «неравно», так что при всех возможных переименованиях в матрице ролей будут сохраняться значения отношений между всеми парами объектов из выборки в виде символов и .
Как и в предыдущем случае, будем в качестве меры расстояния между объектами и использовать разницу ролей, которую они играют среди объектов множества , т. е. разницу их отношений ко всем остальным объектам из . При этом будем пользоваться правилом
![]()

Эта мера расстояния в шкале наименований удовлетворяет требованиям а)-д). Как отмечено в , такая мера может быть найдена и без построения матрицы ролей, а прямо через числа и , указывающие, сколько в выборке имеется объектов с именем и с именем соответственно:
Пример, подтверждающий сказанное, приведен в табл. 5, в которой данные в шкале наименований имеют следующие значения: , так что , , .
Таблица 5. Матрица ролей в шкале наименований
|
По типу евклидова расстояния:
Меры такого типа удовлетворяют всем требованиям а)-д). |
1.1.5. Данные и расстояния в пространствах произвольной природы
Как показано выше, исходные статистические данные могут иметь разнообразную математическую природу, являться элементами разнообразных пространств – конечномерных, функциональных, бинарных отношений, множеств, нечетких множеств и т.д. Следовательно, центральной частью прикладной статистики является статистика в пространствах произвольной природы. Эта область прикладной статистики сама по себе не используется при анализе конкретных данных. Это очевидно, поскольку конкретные данные всегда имеют вполне определенную природу. Однако общие подходы, методы, результаты статистики в пространствах произвольной природы представляют собой научный инструментарий, готовый для использования в каждой конкретной области.
Статистика в пространствах произвольной природы. Много ли общего у статистических методов анализа данных различной природы? На этот естественный вопрос можно сразу же однозначно ответить – да, очень много. Такой ответ будет постоянно подтверждаться и конкретизироваться на протяжении всего учебника. Несколько примеров приведем сразу же.
Прежде всего отметим, что понятия случайного события, вероятности, независимости событий и случайных величин являются общими для любых конечных вероятностных пространств и любых конечных областей значений случайных величин (см. главы 1.2 и 2.1). Поскольку все реальные явления и процессы описываются с помощью математических объектов из конечных множеств, сказанное выше означает, что конечных вероятностных пространств и дискретных случайных величин (точнее, величин, принимающих значения в конечном множестве) достаточно для всех практических применений. Переход к непрерывным моделям реальных явлений и процессов оправдан только тогда, когда этот переход облегчает проведение рассуждений и выкладок. Например, находить определенные интегралы зачастую проще, чем вычислять значения сумм. Не могу не отметить, что приведенные соображения о взаимосоотнесении дискретных и непрерывных математических моделей автор услышал более 30 лет назад от академика А.Н.Колмогорова (ясно, что за конкретную формулировку несет ответственность автор настоящего учебника).
Основные проблемы прикладной статистики – описание данных, оценивание, проверка гипотез – также в своей существенной части могут быть рассмотрены в рамках статистики в пространствах произвольной природы. Например, для описания данных могут быть использованы эмпирические и теоретические средние, плотности вероятностей и их непараметрические оценки, регрессионные зависимости. Правда, для этого пространства произвольной природы должны быть снабжены соответствующим математическим инструментарием – расстояниями (показателями близости, мерами различия) между элементами рассматриваемых пространств.
Популярный в настоящее время метод оценивания параметров распределений – метод максимального правдоподобия – не накладывает каких-либо ограничений на конкретный вид элементов выборки. Они могут лежать в пространстве произвольной природы. Математические условия касаются только свойств плотностей вероятности и их производных по параметрам. Аналогично положение с методом одношаговых оценок, идущим на смену методу максимального правдоподобия (см. главу 2.2). Асимптотику решений экстремальных статистических задач достаточно изучить для пространств произвольной природы, а затем применять в каждом конкретном случае , когда задачу прикладной статистики удается представить в оптимизационном виде. Общая теория проверки статистических гипотез также не требует конкретизации математической природы рассматриваемых элементов выборок. Это относится, например, к лемме Неймана-Пирсона или теории статистических решений. Более того, естественная область построения теории статистик интегрального типа – это пространства произвольной природы (см. главу 2.3).
Совершенно ясно, что в конкретных областях прикладной статистики накоплено большое число результатов, относящимся именно к этим областям. Особенно это касается областей, исследования в которых ведутся сотни лет, в частности, статистики случайных величин (одномерной статистики). Однако принципиально важно указать на «ядро» прикладной статистики – статистику в пространствах произвольной природы. Если постоянно «держать в уме» это ядро, то становится ясно, что, например, многие методы непараметрической оценки плотности вероятности или кластер-анализа, использующие только расстояния между объектами и элементами выборки, относятся именно к статистике объектов произвольной природы, а не к статистике случайных величин или многомерному статистическому анализу. Следовательно, и применяться они могут во всех областях прикладной статистики, а не только в тех, в которых «родились».
Расстояния (метрики). В пространствах произвольной природы нет операции сложения, поэтому статистические процедуры не могут быть основаны на использовании сумм. Поэтому используется другой математический инструментарий, использующий понятия типа расстояния.
Как известно, расстоянием в пространстве Х называется числовая функция двух переменных d (x , y ), x є X , y є X , определенная на этом пространстве, т.е. в стандартных обозначениях d : X 2 → R 1 , где R 1 – прямая, т.е. множество всех действительных чисел. Эта функция должна удовлетворять трем условиям (иногда их называют аксиомами):
1) неотрицательности: d (x ,y ) > 0, причем d (x ,x ) = 0, для любых значений x є X , y є X ;
2) симметричности: d (x ,y ) = d (y ,x ) для любых x є X , y є X ;
3) неравенства треугольника: d (x ,y ) + d (y,z ) > d (x ,z ) для любых значений x є X , y є X , z є X.
Для термина «расстояние» часто используется синоним – «метрика».
Пример 1. Если d (x ,x ) = 0 и d (x ,y ) = 1 при x ≠ y для любых значений x є X , y є X , то, как легко проверить, функция d (x ,y ) – расстояние (метрика). Такое расстояние естественно использовать в пространстве Х значений номинального признака: если два значения (например, названные двумя экспертами) совпадают, то расстояние равно 0, а если различны – то 1.
Пример 2. Расстояние, используемое в геометрии, очевидно, удовлетворяет трем приведенным выше аксиомам. Если Х – это плоскость, а х (1) и х (2) – координаты точки x є X в некоторой прямоугольной системе координат, то эту точку естественно отождествить с двумерным вектором (х (1), х (2)). Тогда расстояние между точками х = (х (1), х (2)) и у = (у (1), у (2)) согласно известной формуле аналитической геометрии равно
Пример 3 . Евклидовым расстоянием в пространстве R k векторов вида x = (x (1), x (2), …, x (k)) и y = (y (1), y (2), …, y (k )) размерности k называется

В примере 2 рассмотрен частный случай примера 3 с k = 2.
Пример 4. В пространстве R k векторов размерности k используют также так называемое «блочное расстояние», имеющее вид
![]()
Блочное расстояние соответствует передвижению по городу, разбитому на кварталы горизонтальными и вертикальными улицами. В результате можно передвигаться только параллельно одной из осей координат.
Пример 5. В пространстве функций, элементами которого являются функции х = x (t ), у = y (t ), 0< t < 1, часто используют расстояние Колмогорова
![]()
Пример 6. Пространство функций, элементами которого являются функции х = x (t ), у = y (t ), 0< t < 1, превращают в метрическое пространство (т.е. в пространство с метрикой), вводя расстояние

Это пространство обычно обозначают L p , где параметр p > 1 (при p < 1 не выполняются аксиомы метрического пространства, в частности, аксиома треугольника).
Пример 7. Рассмотрим пространство квадратных матриц порядка k . Как ввести расстояние между матрицами А = ||a (i ,j )|| и B = ||b (i ,j )||? Можно сложить расстояния между соответствующими элементами матриц:
![]()
Пример 8. Предыдущий пример наводит на мысль о следующем полезном свойстве расстояний. Если на некотором пространстве определены два или больше расстояний, то их сумма – также расстояние.
Пример 9 . Пусть А и В – множества. Расстояние между множествами можно определить формулой
![]()
Здесь μ – мера на рассматриваемом пространстве множеств, Δ – символ симметрической разности множеств,
Если мера – так называемая считающая, т.е. приписывающая единичный вес каждому элементу множества, то введенное расстояние есть число несовпадающих элементов в множествах А и В .
Пример 10. Между множествами можно ввести и другое расстояние:
![]()
В ряде задач прикладной статистики используются функции двух переменных, для которых выполнены не все три аксиомы расстояния, а только некоторые. Их обычно называют показателями различия, поскольку чем больше различаются объекты, тем больше значение функции. Иногда в том же смысле используют термин «мера близости». Он менее удачен, поскольку большее значение функции соответствует меньшей близости.
Чаще всего отказываются от аксиомы, требующей выполнения неравенства треугольника, поскольку это требование не всегда находит обоснование в конкретной прикладной ситуации.
Пример 11. В конечномерном векторном пространстве показателем различия является
![]()
(сравните с примером 3).
Показателями различия, но не расстояниями являются такие популярные в прикладной статистике показатели, как дисперсия или средний квадрат ошибки при оценивании.
Иногда отказываются также и от аксиомы симметричности.
Пример 12. Показателем различия чисел х и у является
![]()
Такой показатель различия используют в ряде процедур экспертного оценивания.
Что же касается первой аксиомы расстояния, то в различных постановках прикладной статистики ее обычно принимают. Вполне естественно, что наименьший показатель различия должен достигаться, причем именно на совпадающих объектах. Имеет ли смысл это наименьшее значение делать отличным от 0? Вряд ли, поскольку всегда можно добавить одну и ту же константу ко всем значениям показателя различия и тем самым добиться выполнения первой аксиомы.
В прикладной статистике используются самые разные расстояния и показатели различия, о них пойдет речь в соответствующих разделах учебника.
| Предыдущая |
РАССТОЯНИЕ МЕЖДУ ОБЪЕКТАМИ (МЕТРИКА)
Введём понятие "расстояние между объектами". Данное понятие является интегральной мерой сходства объектов между собой. Расстоянием между объектами в пространстве признаков называется такая величина d ij , которая удовлетворяет следующим аксиомам:
- 1. d ij > 0 (неотрицательность расстояния)
- 2. d ij = d ji (симметрия)
- 3. d ij + d jk > d ik (неравенство треугольника)
- 4. Если d ij не равно 0, то i не равно j (различимость нетождественных объектов)
- 5. Если d ij = 0, то i = j (неразличимость тождественных объектов)
Меру близости (сходства) объектов удобно представить как обратную величину от расстояния между объектами. В многочисленных изданиях посвященных кластерному анализу описано более 50 различных способов вычисления расстояния между объектами. Кроме термина "расстояние" в литературе часто встречается и другой термин - "метрика", который подразумевает метод вычисления того или иного конкретного расстояния. Наиболее доступно для восприятия и понимания в случае количественных признаков является так называемое "евклидово расстояние" или "евклидова метрика". Формула для вычисления такого расстояния:
В данной формуле использованы следующие обозначения:
- · d ij - расстояние между i-тым и j-тым объектами;
- · x ik - численное значение k-той переменной для i-того объекта;
- · x jk - численное значение k-той переменной для j-того объекта;
- · v - количество переменных, которыми описываются объекты.
Таким образом, для случая v=2, когда мы имеем всего два количественных признака, расстояние d ij будет равно длине гипотенузы прямоугольного треугольника, которая соединяет собой две точки в прямоугольной системе координат. Эти две точки будут отвечать i-тому и j-тому наблюдениям выборки. Нередко вместо обычного евклидового расстояния используют его квадрат d 2 ij . Кроме того, в ряде случаев используется "взвешенное" евклидово расстояние, при вычислении которого для отдельных слагаемых используются весовые коэффициенты. Для иллюстрации понятия евклидовой метрики используем простой обучающий пример. Матрица данных, приведенная ниже в таблице, состоит из 5 наблюдений и двух переменных.
Таблица 1
Матрица данных из пяти наблюдаемых проб и двух переменных.
Используя евклидову метрику, вычислим матрицу межобъектных расстояний, состоящую из величин d ij - расстояние между i-тым и j-тым объектами. В нашем случае i и j - номер объекта, наблюдения. Поскольку объем выборки равен 5, то соответственно i и j могут принимать значения от 1 до 5. Очевидно также, что количество всех возможных по парных расстояний будет равно 5*5=25. Действительно, для первого объекта это будут следующие расстояния: 1-1; 1-2; 1-3; 1-4; 1-5. Для объекта 2 также будет 5 возможных расстояний: 2-1; 2-2; 2-3; 2-4; 2-5 и т.д. Однако число различных расстояний будет меньше 25, поскольку необходимо учесть свойство неразличимости тождественных объектов - d ij = 0 при i = j. Это означает, что расстояние между объектом №1 и тем же самым объектом №1 будет равно нулю. Такие же нулевые расстояния будут и для всех остальных случаев i = j. Кроме того, из свойства симметрии следует, что d ij = d ji для любых i и j. Т.е. расстояние между объектами №1 и №2 равно расстоянию между объектами №2 и №1.
Весьма напоминает выражение для евклидового расстояния так называемое обобщенное степенное расстояние Минковского, в котором в степенях вместо двойки используется другая величина. В общем случае эта величина обозначается символом "р".
При р = 2 мы получаем обычное Евклидово расстояния. Так выражение для обобщенной метрики Минковского имеет вид:

Выбор конкретного значения степенного показателя "р" производится самим исследователем.
Частным случаем расстояния Минковского является так называемое манхэттенское расстояние, или "расстояние городских кварталов" (city-block), соответствующее р=1:

Таким образом, манхэттенское расстояние является суммой модулей разностей соответствующих признаков объектов. Устремив p к бесконечности, мы получаем метрику "доминирования", или Sup-метрику:

которую можно представить также в виде d ij = max| x ik - x jk |.
Метрика Минковского фактически представляет собой большое семейство метрик, включающее и наиболее популярные метрики. Однако существуют и методы вычисления расстояния между объектами, принципиально отличающиеся от метрик Минковского. Наиболее важное из них так называемое расстояние Махаланобиса, которое имеет достаточно специфические свойства. Выражение для данной метрики:
Здесь через X i и X j обозначены вектор-столбцы значений переменных для i-того и j-того объектов. Символ Т в выражении (X i - X j ) Т обозначает так называемую операцию транспонирования вектора. Символом S обозначена общая внутригрупповая дисперсионно-ковариационная матрица. А символ -1 над S означает, что необходимо обратить матрицу S . В отличие от метрики Минковского и евклидовой метрики, расстояние Махаланобиса через матрицу дисперсий-ковариаций S связано с корреляциями переменных. Когда корреляции между переменными равны нулю, расстояние Махаланобиса эквивалентно квадрату евклидового расстояния.
В случае использования дихотомических (имеющих всего два значения) качественных признаков широко используется расстояние Хемминга

равное числу несовпадений значений соответствующих признаков для рассматриваемых i-того и j-того объектов.
Во взаимодействии человека с окружающей средой восприятие пространства играет большую роль, являясь условием ориентировки. Представляет оно собой отражение объективно существующего пространства и включает в себя:
- Восприятие отдаления;
- Восприятие расстояния между объектами;
- Восприятие направления;
- Восприятие величины объектов;
- Восприятие формы объектов.
Тело человека тоже взаимодействует со средой и имеет свою систему координат, а сам человек имеет определенное место в пространстве. Среди всего, что воспринимает человек, восприятие пространства занимает особое место. В пространстве находятся все объекты материального мира и свершаются различные природные и социальные явления.
К пространственным свойствам одного объекта относятся величина и форма, а если этот же объект рассматривается в связи с другими объектами, то добавляется положение в пространстве, направление, расстояние. В пространственной ориентировке особую роль выполняет двигательный анализатор. С его помощью устанавливается взаимодействие между различными анализаторами. Бинокулярное зрение, бинауральный слух, бимануальное осязание, дириническое обоняние относят к специальным механизмам пространственной ориентировки.
Восприятие пространства в психологии рассматривается как отражение пространственных характеристик объектов внешней среды.
Зрительные восприятия одновременно базируются и на зрительных, и на двигательных ощущениях. Слуховые и обонятельные восприятия играют вспомогательную роль, а двигательные и осязательные – на близких расстояниях.
Зрение человека имеет способность различать удаленность предметов на расстоянии до 2,5 км. Предметы, расположенные дальше этого предела, воспринимаются человеком как размещенные на одной плоскости, звезды, например, представляются «размещенными» на внутренней поверхности сферы на одинаковом расстоянии от точки наблюдения, т.е. от глаз человека.
Визуальное восприятие удаленности обеспечивается бинокулярным зрением, т.е. видение двумя глазами. Ощущение удаленности появляется, потому что возникают зрительные различия в зрительных ощущениях от каждого глаза. Данные эффекты имеют физиологическую основу:
- Раздраженные одновременно точки на сетчатках левого и правого глаза не совпадают;
- Мускульные ощущения глазных мышц.
Чтобы определить расстояние до нескольких известных объектов чаще всего используют результат их взаимного соотнесения, если, например, футбольный мяч меньше теннисного, то совершенно понятно, что он расположен значительно дальше.
Определять расстояния до предметов человек может не только с помощью зрения, но еще с помощью слуха и обоняния, хотя вероятность становится меньше. Точность отражения в данном случае будет зависеть от индивидуальных особенностей человека. Двигательное восприятие тоже может дать определенную информацию о расстоянии, но только в пределах досягаемости руки или ноги. В качестве примера можно назвать перемещение человека в темной комнате – во избежание столкновения обычно вперед вытягивается рука или обшаривается пол ногой.
Восприятие величины
Величина предмета, которую воспринимает человек, зависит от их угловой величины и расстояния, с которого этот предмет наблюдается. Если знать величину предмета, то по его угловой величине можно определить расстояние до него. И, наоборот, зная, на каком расстоянии находится предмет, по его угловым размерам, определяется величина предмета.
Например, если смотреть в бинокль, зная величину предметов, человек видит их приблизившимися, но не увеличенными, а если на печатный шрифт смотреть в лупу, то буквы будут увеличенными, но не приблизившимися. Таким образом, в результате опыта развивается способность глаза сравнивать пространственные величины, направления и удаленность объекта от наблюдателя. Эта способность получила название глазомера.
Глазомер человека трехмерный, что значит, имеет способность сравнивать пространственные формы, расположенные в трех измерениях, включая плоскостный и глубинный. Сравнение это может относиться к линиям, поверхностям и объемам.
Плоскостный глазомер дает возможность сравнивать формы на плоскости, которая расположена в направлении, перпендикулярной зрительной оси.
Глубинный глазомер способен сравнивать пространственные формы в глубину.
Восприятие формы
Плоскостная форма предмета и её восприятие предполагает отчетливое различение его очертаний и границ, зависит это от четкости изображения, получающегося на сетчатке глаза.
На основании проведенных исследований константность формы объясняется действием периферических и центральных факторов. Восприятие трехмерных предметов насыщенно глубинными ощущениями и предметы, расположенные близко, кажутся несколько меньше. Действие фактора компенсирует действие перспективных сокращений.
С другой стороны, в константности восприятия формы, существенную роль играют представления, прошлый опыт. В экспериментах с псевдоскопом роль прошлого опыта выявлялась очень наглядно. Восприятие псевдоскоп ставит в условия обратной перспективы – ближние точки пространства переходят в дальние, а дальние в ближние. Следовательно, все вогнутые предметы должны восприниматься как выпуклые, а выпуклые, наоборот, как вогнутые. В результате получилось, что формы экспонатов, не закрепленных опытом, действительно так и воспринимаются.
Явление константности не срабатывает при восприятии объектов, которые находятся на очень большом удалении, у воспринимаемого объекта сглаживаются острые углы. Исчезают некоторые мелкие детали. Интересно, что лицо человека никогда не воспринимается в обратной перспективе.
Действие центральных факторов корригируют данные периферических раздражений и фактическое восприятие предметов обусловлено не только наличными периферическими раздражениями, но и прошлым опытом.
Восприятие направления
Данное восприятие является одним из важных моментов пространственного различения. Направление, в котором человек видит объект, определяется местом его изображения на сетчатке глаза и положением тела относительно окружающих предметов. Относительно горизонтальной плоскости Земли, тело человека занимает вертикальное положение. Данное положение и будет являться исходным для определения направления. В восприятии направления, кроме зрительных ощущений, большую роль играют кинестезические ощущения движений глаз, рук и статические ощущения – ощущения равновесия и положения тела.
Направление видимого предмета при бинокулярном зрении определяется законом тождественного направления, по которому раздражители, падающие на сетчатку, видятся в одном и том же направлении. Это направление дается линией, идущей как бы от одного «циклопического глаза», расположенного посередине лба.
Предметы, на которые смотрит человек, на сетчатке глаза перевернуты. Перемещение наблюдаемого объекта вызывает перемещение сетчаточного изображения в обратном направлении. Но, человек воспринимает предметы, как движущиеся, так и неподвижные вовсе не в искаженном виде, а такими, какими оптическая система глаз передает их на сетчатку. Происходит это благодаря сочетанию зрительных ощущений с тактильными, кинестезическими и другими сигналами.
При бинауральном слушании осуществляется восприятие направления звука. В основе дифференцировки направлений звука лежит разность во времени поступления сигналов в кору головного мозга от обоих ушей. Звуки могут локализоваться в разном направлении – по вертикали и горизонтали. В первом случае, как показали эксперименты, для восприятия пространственного расположения звука необходимы движения головы. Механизм локализации звука, таким образом, учитывает не только слуховые сигналы, но и данные других анализаторных систем.
 Могильники Чернобыля: радиоактивные отходы зоны отчуждения Где находится техника чернобыля
Могильники Чернобыля: радиоактивные отходы зоны отчуждения Где находится техника чернобыля Девочка заговорила на иностранном языке после комы
Девочка заговорила на иностранном языке после комы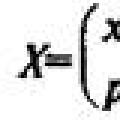 Сравнение законов распределения вероятностей
Сравнение законов распределения вероятностей