Простейшие формулы численного интегрирования прямоугольников трапеций. Формулы численного интегрирования. Общие формулы Ньютона-Котеса

Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x) . Такой функцией обычно является полином (кусочный полином) . То есть:
,
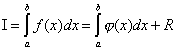где – априорная погрешность метода на интервале интегрирования,
а r(x) – априорная погрешность метода на отдельном шаге интегрирования.

Обзор методов интегрирования.

Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными ).

Метод прямоугольников.

Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.

Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = x i .

Рассмотрим диапазон интегрирования от x i до x i +h , где h – шаг интегрирования.

Вычислим …=

= = . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.

В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид

.

Здесь n – число разбиений интервала интегрирования, . Для справедливости существования этой оценки необходимо существование непрерывной f"(x).

Метод средних прямоугольников . Здесь на каждом интервале значение функции считается в точке , то есть . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

.

Метод трапеций.

Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка.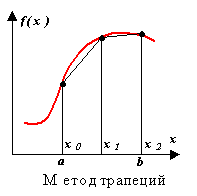

На единичном интервале
.
В случае равномерной сетки (h = const)

При этом , а . Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Особенности поведения погрешности.

Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимост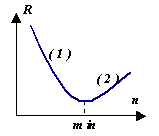и от числа n разбиений интервала (то есть при шаг . На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя R min , которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R .

Уточняющая формула Ромберга.

Метод Ромберга заключается в последовательном уточнении значения интеграла при кратном увеличении числа разбиений. В качестве базовой может быть взята формула трапеций с равномерным шагом h .
Обозначим интеграл с числом разбиений n = 1 как .
Уменьшив шаг в два раза, получим .
Если последовательно уменьшать шаг в 2 n раз, получим рекуррентное соотношение для расчета .

Пусть мы вычислили четыре раза интеграл с n от 1 до 4. Представим следующий треугольник:
R(1;1)
R(2;1) R(2;2)
R(3;1) R(3;2) R(3;3)
R(4;1) R(4;2) R(4;3) R(4;4)

В первом столбце стоят значения интеграла, полученные при последовательном удвоении числа интервалов. Следующие столбцы – результаты уточнения значения интеграла по следующей рекуррентной формуле:

Правое нижнее значение в треугольнике – искомое уточненное значение интеграла.

Метод Симпсона.

Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) ­– полином).

Рассмотрим два шага интегрирования (h = const = x i+1 – x i ), то есть три узла x 0 , x 1 , x 2 , через которые проведем параболу, воспользовавшись уравнением Ньютона:
.
Пусть z = x - x 0 ,
тогда

Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:

.

Ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых x=a\,\! и x=b\,\! , где a\,\! и b\,\! - пределы интегрирования (см. рисунок).

Необходимость применения численного интегрирования чаще всего может быть вызвана отсутствием у представления в и, следовательно, невозможностью аналитического вычисления значения определенного интеграла по . Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.

Одномерный случай

Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида

I \approx \sum_{i=1}^{n} w_i\, f(x_i),

где n\,\! - число точек, в которых вычисляется значение подынтегральной функции. Точки x_i\,\! называются узлами метода, числа w_i\,\! - весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответсвенно методы , и (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.

Метод прямоугольников

Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой точке отрезка \left\,\! . Наиболее часто используются значения функции в середине отрезка и на его концах. Соответсвующие модификации носят названия методов средних прямоугольников , левых прямоугольников и правых прямоугольников . Формула для приближенного вычисления значения определенного интеграла методом прямоугольников имеет вид

I \approx f(x) (b-a) ,

где x=\frac{\left(a+b\right)}{2} , a\,\! или b\,\! , соответсвенно.

Метод трапеций

Если через концы отрезка интегрирования провести прямую, получим метод трапеций . Из геометрических соображений легко получить

I \approx \frac{f(a)+f(b)}{2} (b-a) .

Метод парабол

Использовав три точки отрезка интегрирования можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид

I \approx \frac{b-a}{6}\left(f(a)+4f\left(\frac{a+b}{2}\right)+f(b)\right) .

Увеличение точности

Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.

Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.

При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для любого численного метода.

Приведенные выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется .

Метод Гаусса

Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий (1, 1 и 3, соответственно). Если мы можем выбирать точки, в которых мы вычисляем значения функции f(x)\,\! , то можно при том же количестве вычислений подынтегральной функции получить методы более высокого порядка точности. Так для двух (как в методе трапеций) вычислений значений подынтегральной функции, можно получить метод уже не 1-го, а 3-го порядка точности:

I \approx \frac{b-a}{2}\left(f\left(\frac{a+b}{2} - \frac{b-a}{2\sqrt{3}} \right)+f\left(\frac{a+b}{2} + \frac{b-a}{2\sqrt{3}} \right) \right) .

В общем случае, используя n\,\! точек, можно получить метод с порядком точности 2n-1\,\! . Значения узлов метода Гаусса по n\,\! точкам являются корнями полинома Лежандра степени n\,\! .

Значения узлов метода Гаусса и их весов приводятся в справочниках специальных функций. Наиболее известен метод Гаусса по пяти точкам.

Метод Гаусса-Кронрода

Недостаток метода Гаусса состоит в том, что он не имеет легкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша точности, в отличие от простых методов, где точность увеливается в разы при каждом новом разбиении. Кронродом был предложен следующий метод оценки значения интеграла

I \approx \sum_{i=1}^{n} a_i\, f(x_i) + \sum_{i=1}^{n+1} b_i\, f(y_i) ,

где x_i\,\! - узлы метода Гаусса по n\,\! точкам, а 3n+2\,\! параметров a_i\,\! , b_i\,\! , y_i\,\! подобраны таким образом, чтобы порядок точности метода был равен 3n+1\,\! .

Тогда для оценки погрешности можно использовать эмпирическую формулу

\Delta = \left(200 |I - I_G|\right)^{1.5} ,

где I_G\,\! - значение интеграла, оценненое методом Гаусса по n\,\! точкам. Библиотеки [

Страница 1

Кафедра «Высшей математики»
Реферат:

Выполнил: Матвеев Ф.И.
Проверила: Бурлова Л.В.

Улан-Удэ.2002

1.Численные методы интегрирования

2.Вывод формулы Симпсона

3.Геометрическая иллюстрация

4.Выбор шага интегрирования

5.Примеры

1. Численные методы интегрирования
Задача численного интегрирования заключается в вычислении интеграла

посредством ряда значений подынтегральной функции
.

Задачи численного интегрирования приходится решать для функций, заданных таблично, функцией, интегралы от которых не берутся в элементарных функциях, и т.д. Рассмотрим только функции одной переменной.

Вместо функции, которую требуется проинтегрировать, проинтегрируем интерполяционный многочлен. Методы, основанные на замене подынтегральной функции интерполяционным многочленом, позволяют по параметрам многочлена оценить точность результата или же по заданной точности подобрать эти параметры.

Численные методы условно можно сгруппировать по способу аппроксимации подынтегральной функции.

Методы Ньютона-Котеса основаны на аппроксимации функции
полиномом степени . Алгоритм этого класса отличается только степенью полинома. Как правило, узлы аппроксимирующего полинома – равноотносящие.

Методы сплайн-интегрирования базируются на аппроксимации функции
сплайном-кусочным полиномом.

В методах наивысшей алгебраической точности (метод Гаусса) используются специально выбранные неравноотносящие узлы, обеспечивающие минимальную погрешность интегрирования при заданном (выбранном) количестве узлов.

Методы Монте-Карло используются чаще всего при вычислении кратных интегралов, узлы выбираются случайным образом, ответ носит вероятностный характер.

суммарная погрешность

погрешность усечения

погрешность округления

Независимо от выбранного метода в процессе численного интегрирования необходимо вычислить приближенное значение интеграла и оценить погрешность. Погрешность уменьшается при увеличении n-количества

разбиений отрезка
. Однако при этом возрастает погрешность округления

за счет суммирования значений интегралов, вычисленных на частичных отрезках.

Погрешность усечения зависит от свойств подынтегральной функции и длины частичного отрезка.
2. Вывод формулы Симпсона
Если для каждой пары отрезков
построить многочлен второй степени, затем проинтегрировать его и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона.

Рассмотрим подынтегральную функцию
на отрезке
. Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с
в точках :

Проинтегрируем
:

Формула:

и называется формулой Симпсона.

Полученное для интеграла
значение совпадает с площадью криволинейной трапеции, ограниченной осью , прямыми
,
и параболой, проходящей через точки

Оценим теперь погрешность интегрирования по формуле Симпсона. Будем считать, что у на отрезке
существуют непрерывные производные
. Составим разность

К каждому из этих двух интегралов уже можно применить теорему о среднем, поскольку
непрерывна на
и функция неотрицательна на первом интервале интегрирования и неположительна на втором (то есть не меняет знака на каждом из этих интервалов). Поэтому:

(мы воспользовались теоремой о среднем, поскольку
- непрерывная функция;
).

Дифференцируя
дважды и применяя затем теорему о среднем, получим для
другое выражение:

, где

Из обеих оценок для
следует, что формула Симпсона является точной для многочленов степени не выше третьей. Запишем формулу Симпсона, напрмер, в виде:

,
.

Если отрезок
интегрирования слишком велик, то его разбивают на
равных частей (полагая
), после чего к каждой паре соседних отрезков
,
,...,
применяют формулу Симпсона, именно:

Запишем формулу Симпсона в общем виде:

(1)

(2)

Погрешность формулы Симпсона - метода четвертого порядка:

,
(3)

Так как метод Симпсона позволяет получить высокую точность, если
не слишком велика. В противном случае метод второго порядка может дать большую точность.

Например, для функции форма трапеции при
для
дает точный результат
, тогда как по формуле Симпсона получаем

3. Геометрическая иллюстрация

На отрезке
длиной 2h строится парабола, проходящая через три точки
,
. Площадь под параболой, заключенная между осью OX и прямыми
, принимают равной интегралу
.

Особенностью применения формулы Симпсона является тот факт, что число разбиений отрезка интегрирования - четное.

Если же количество отрезков разбиения - нечетное, то для первых трех отрезков следует применить формулу, использующую параболу третьей степени, проходящую через четыре первые точки, для аппроксимации подынтегральной функции.

(4)

Это формула Симпсона «трех восьмых».

Для произвольного отрезка интегрирования
формула (4) может быть «продолжена»; при этом число частичных отрезков должно быть кратно трем (
точек).

, m=2,3,... (5)

- целая часть

Можно получить формулы Ньютона-Котеса старших порядков:

(6)

- количество отрезков разбиения;

- степень используемого полинома;

- производная -го порядка в точке
;

- шаг разбиения.

В таблице 1 выписаны коэффициенты
. Каждая строка соответствует одному набору промежутков
узлами для построения многочлена k-ой степени. Чтобы воспользоваться этой схемой для большего количества наборов (например, при k=2 и n=6), нужно «продолжить» коэффициенты, а затем сложить их.

Таблица 1:

k	C0	A0	a1	a2	a3	a4	a5	a6
2		1	4	1
				1	4	1
						1	4	1
		1	4	2		2	4	1	

Алгоритм оценки погрешности формул трапеции и Симпсона можно записать в виде:
(7),

где - коэффициент, зависящий от метода интегрирования и свойств подынтегральной функции;

h - шаг интегрирования;

p - порядок метода.

Правило Рунге применяют для вычисления погрешности путем двойного просчета интеграла с шагами h и kh.

(8)

(8) - апостериорная оценка. Тогда Iуточн.= +Ro (9),
уточненное значение интеграла
.

Если порядок метода неизвестен, необходимо вычислить I в третий раз с шагом
, то есть:

из системы трех уравнений:

с неизвестными I,А и p получаем:

(10)

Из (10) следует
(11)

Таким образом, метод двойного просчета, использованный необходимое число раз, позволяет вычислить интеграл с заданной степенью точности. Выбор необходимого числа разбиений осуществляется автоматически. Можно при этом использовать многократное обращение к подпрограммам соответствующих методов интегрирования, не изменяя алгоритмов этих методов. Однако для методов, использующих равноотносящие узлы, удается модифицировать алгоритмы и уменьшить вдвое количество вычислений подынтегральной функции за счет использования интегральных сумм, накопленных при предыдущих кратных разбиениях интервала интегрирования. Два приближенных значения интеграла
и
, вычисляемые по методу трапеции с шагами и
, связаны соотношением:

Аналогично, для интегралов, вычисленных по формуле с шагами и
, справедливы соотношения:

,

(13)

4. Выбор шага интегрирования
Для выбора шага интегрирования можно воспользоваться выражением остаточного члена. Возьмем, например, остаточный член формулы Симпсона:

Если 

, то 

.

По заданной точности  метода интегрирования из последнего неравенства определяем подходящий шаг.

,
.

Однако такой способ требует оценки
(что на практике не всегда возможно). Поэтому пользуются другими приемами определения оценки точности, которые по ходу вычислений позволяют выбрать нужный шаг h.

Разберем один из таких приемов. Пусть

,

где - приближенное значение интеграла с шагом . Уменьшим шаг в два раза, разбив отрезок
на две равные части
и
(
).

Предположим теперь, что
меняется не слишком быстро, так что
почти постоянна: . Тогда
и
, откуда
, то есть
.

Отсюда можно сделать такой вывод: если
, то есть если
,
, а - требуемая точность, то шаг подходит для вычисления интеграла с достаточной точностью. Если же
, то расчет повторяют с шагом и затем сравнивают
и
и т.д. Это правило называется правилом Рунге.

Однако при применении правила Рунге необходимо учитывать величину погрешности вычислений: с уменьшением абсолютная погрешность вычислений интеграла увеличивается (зависимость
от обратно пропорциональная) и при достаточно малых может оказаться больше погрешности метода. Если превышает
, то для данного шага применять правило Рунге нельзя и желаемая точность не может быть достигнута. В таких случаях необходимо увеличивать значение .

При выводе правила Рунге вы существенно пользовались предположением, что
. Если имеется только таблица значений , то проверку
«на постоянство» можно сделать непосредственно по таблице Дальнейшее развитие приведенных алгоритмов позволяет перейти к адаптивным алгоритмам, в которых за счет выбора различного шага интегрирования в разных частях отрезка интегрирования в зависимости от свойств
уменьшается количество вычислений подынтегральной функции.

Другая схема уточнения значений интеграла - процесс Эйтнена. Производится вычисление интеграла с шагами
, причем
. Вычисление значений . Тогда
(14).

За меру точности метода Симпсона принимают величину:

5. Примеры
Пример 1. Вычислить интеграл
по формуле Симпсона, если
задана таблицей. Оценить погрешность.

Таблица 3.

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
	1	0.995	0.98	0.955	0.921	0.878	0.825	0.765	0.697

Решение: Вычислим по формуле (1) при
и
интеграл .

По правилу Рунге получаем
Принимаем .

Пример 2. Вычислить интеграл
.

Решение: Имеем
. Отсюда h=
=0.1. Результаты вычислений приведены в таблице 4.

Таблица 4.

Вычисление интеграла по формуле Симпсона

i
0	0		y0=1,00000
1	0.1	0,90909
2	0.2		0,83333
3	0.3	0,76923
4	0.4		0,71429
5	0.5	0,66667
6	0.6		0,62500
7	0.7	0,58824
8	0.8		0,55556
9	0,9	0,52632
10	1,0		0,50000=yn
		3,45955(1)	2,72818(2)

По формуле Симпсона получим:

Подсчитаем погрешность полученного результата. Полная погрешность складывается из погрешностей действий и остаточного члена . Очевидно:-0,289687

4

2,35

-0,70271

-0,299026

2,4

-0,73739

-0,307246

2

2,45

-0,77023

-0,314380

2,5

-0,80114

-0,320465

4

2,55

-0,83005

-0,325510

2,6

-0,85689

-0,329573

2

2,65

-0,88158

-0,332672

2,7

-0,90407

-0,334841

4

2,75

-0,92430

-0,336109

 3.

численное интегрирование формула программирование

Введение

1. Методы численного интегрирования

2. Квадратурные формулы

3. Автоматический выбор шага интегрирования

Заключение

Библиографический список

Введение

Цель реферата состоит в изучение и сравнительный анализ методов численного интегрирования функций; реализация этих методов в виде машинных программ на языке высокого уровня и практическое решение задач численного интегрирования на ЭВМ.

При решении инженерных задач часто возникает необходимость в вычислениях значений определенного интеграла вида

. (1)

Если функция непрерывна на отрезке [a , b ] и ее первообразная может быть определена через известную функцию, то вычисление такого интеграла производится по формуле Ньютона – Лейбница:

.

В инженерных задачах получить значение интеграла в аналитическом виде удается редко. Кроме того, функция f (x ) может быть задана, например, таблицей экспериментальных данных. Поэтому на практике для вычисления определенного интеграла используют специальные методы, в основе которых лежит аппарат интерполирования.

Идея таких методов заключается в следующем. Вместо того, чтобы вычислять интеграл по формуле (1), сначала вычисляют значения функции f (x i ) = y i в некоторых узлах x i Î[a , b ]. Затем выбирается интерполяционный многочлен P (x ), проходящий через полученные точки (x i , y i ), который используется при вычислении приближенного значения интеграла (1):

.

При реализации такого подхода формулы численного интегрирования принимают следующий общий вид:

, (2) - узлы интерполирования, A i – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами.

Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f (х ),осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена R , характеризующего погрешность метода, на которую дополнительно накладывается вычислительная погрешность.

1. Методы численного интегрирования

В прикладных исследованиях часто возникает необходимость вычисления значения определённого интеграла

Как известно из курса математики, аналитически вычисление интеграла можно провести не во всех случаях. И даже в том случае, когда удаётся найти аналитический вид этого интеграла, процедура вычисления даёт приближённый результат, поэтому возникает задача приближенного значения этого интеграла.

Суть приближенного вычисления заключается в двух операциях: 1. в выборе конечного числа вместо n; 2. в выборе точки

в соответствующем отрезке.

В зависимости от выбора

мы получаем различные формулы для вычисления интеграла: Формулы левых и правых прямоугольников (5), (6) (5) (6)

Формула трапеции:

Формула Симпсона

b, a - концы рассматриваемого отрезка.

Для сравнения результатов вычисления вышеизложенными формулами численного интегрирования вычислим 3-мя способами следующий интеграл, разделив отрезок на 6 равных отрезков: h=

По формуле левых прямоугольников:

По формуле трапеции:

По формуле Симпсона:

А результат полученный аналитически равен

=1

Следовательно, можно сделать вывод о том, что численный метод интегрирования по формуле Симпсон является более точным, но используется в общем случае при делении рассориваемого отрезка на чётное число промежутков.

2. Квадратурные формулы

Формулы прямоугольников являются наиболее простыми квадратурными формулами. Разобьем отрезок интегрирования [a, b ] на п равных частей длиной

. Заметим, что величину h называют шагом интегрирования. В точках разбиения х 0 = а , х 1 = a + h , ..., x n = b отметим ординаты y 0 , y 1 ,…, y n кривой f (x ), т.е. вычислим у i = f (x i ), x i = a+ ih = x i -1 + h (i = ). На каждом отрезке длиной h построим прямоугольник со сторонами h и y i , где i = , т.е. по значениям ординат, вычисленных в левых концах отрезков. Тогда площадь криволинейной трапеции, определяющую величину интеграла (1), приближенно можно представить в виде суммы площадей прямоугольников (рис. 1). Отсюда получим формулу прямоугольников:
. (3)

Если при вычислении интегральной суммы брать значения функции f (x ) не в левых, а в правых концах отрезков длиной h , что показано на рис. 1 пунктирной линией, то получим второй вариант формулы прямоугольников:

. (4)

Третий вариант формулы прямоугольников можно получить при использовании значений функции f (x ), вычисленных в средней точке каждого отрезка длины h (рис. 2):

. (5)

Формулы (3), (4) и (4) называют формулами левых, правых и центральных прямоугольников соответственно.

Формула Симпсона. Разобьем интервал интегрирования на 2n равных частей длиной

. На каждом отрезке [x i , x i+2 ] подынтегральную функцию f (х ) заменим параболой, проходящей через точки (x i , y i ), (x i +1 , y i +1), (x i +2 , y i +2). Тогда приближенное значение интеграла определяется формулой Симпсона: . (7)

При вычислениях на ЭВМ более удобна следующая формула:

Метод Симпсона - один из наиболее широко известных и применяемых методов численного интегрирования, он дает точные значения интеграла при интегрировании многочленов до третьего порядка включительно.

Формула Ньютона. Приближенное значение интеграла по формуле Ньютона вычисляется следующим образом:

где число участков разбиения кратно трем, т.е. составляет 3n . При разработке программ для ЭВМ удобнее использовать эквивалентную формулу:

Метод Ньютона дает точные значения интеграла при интегрировании многочленов до четвертого порядка включительно.

3. Автоматический выбор шага интегрирования

В результате расчета по формулам (3) - (8) получают приближенное значение интеграла, которое может отличаться от точного на некоторую величину, называемую погрешностью интегрирования. Ошибка определяется формулой остаточного члена R , различной для каждого из методов интегрирования. Если требуется вычислить значение интеграла с погрешностью, не превышающей e, то необходимо выбрать такой шаг интегрирования h , чтобы выполнялось неравенство R (h ) £e. На практике используют автоматический выбор значения h , обеспечивающего достижение заданной погрешности. Сначала вычисляют значение интеграла I (n ), разбивая интервал интегрирования на п участков, затем число участков удваивают и вычисляют интеграл I (2n ). Процесс вычислений продолжают до тех пор, пока не станет справедливым условие.

Методы численного интегрирования

ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

Лекция-5

Замечание.

Операторы

use linear_operators

означают подключение библиотек стандартных подпрограмм dfimsl и
linear_operators, соответственно.

В библиотеке linear_operators возможно использовать стандартную подпрограмму определения собственных чисел и векторов eig в виде:

lambda=eig(a,v=y),

a – исходная матрица (двумерный массив nxn ),

lambda – вектор собственных чисел (одномерный массив длиной n ),

y – матрица собственных векторов, расположенных по столбцам (двумерный массив nxn ).

Перечисленные массивы должны быть объявлены в программе.

Пусть требуется вычислить определенный интеграл вида

Для многих функций первообразные представляют собой достаточно сложные комбинации элементарных функций, либо вовсе не выражаются через них. В таких случаях использование формулы Ньютона-Лейбница на практике не представляется возможным. Во многих практических случаях достаточно получить значение интеграла с заданной точностью . Для вычисления приближенного значения интеграла существуют формулы численного интегрирования. Суть построения формул численного интегрирования состоит в следующем.

Разобьем отрезок на частей. Для простоты изложения положим эти части одинаковой длины :

Пронумеруем точки разбиения так, как показано на рис. 2.5.1. Имеем:

Рис. 2.5.1. К вопросу о численном интегрировании.

Исходный интеграл (2.5.1) может быть представлен в виде суммы интегралов по полученным в результате разбиения «малым» отрезкам:

. (2.5.2)

Интегралы

вычисляются по приближенным формулам.

Простейшие формулы для приближенного вычисления интегралов по отрезку называются квадратурными формулами . Рассмотрим некоторые из них ниже, а также изучим вопросы их точности. Порядок точности квадратурной формулы определяется степенью полинома (многочлена), для которой эта квадратурная формула точна.

2.5.2. Формула прямоугольников (формула «средних»).

Заменим на i -ом участке интегрируемую функцию постоянной величиной, например, равной ее значению в средней точке (рис. 2.5.2):

Рис. 2.5.2. К интегрированию по формуле прямоугольников.

, где . (2.5.4)

Тогда интеграл на отрезке заменяется площадью прямоугольника, т.е.

, (2.5.5)

и вычисление исходного интеграла сводится к вычислению суммы

. (2.5.6)

Кроме того, часто из практических соображений в качестве в формуле (2.5.6) берется , либо . В результате получаем:

(2.5.7)

– квадратурная формула «левых» прямоугольников;

(2.5.8)

– квадратурная формула «правых» прямоугольников.

Формулы (2.5.7) и (2.5.8) менее точные, чем (2.5.6), но иногда более удобные, например, при численном решении дифференциальных уравнений.

Точность вычисления . Как следует из построения квадратурные формулы прямоугольников дают точный результат интегрирования для функций, постоянных на i -ом участке (). Квадратурная формула «средних» прямоугольников дает точный результат также и для линейных на i -ом отрезке функций. Это утверждение достаточно проверить для простейшей линейной функции .

При точном интегрировании получаем:

,

а при интегрировании по формуле «средних» прямоугольников

Как видно, результаты точного и численного интегрирования совпадают.