Найти площадь интеграл. Площадь криволинейной трапеции. Итак, систематизируем важные моменты этой задачи

В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.

Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.

Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.

Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.

Очередной канун Нового Года... морозная погода и снежинки на оконном стекле... Все это побудило меня вновь написать о... фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.

Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.

Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: "Фракталы - это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией".

Пример1 . Вычислить площадь фигуры, ограниченной линиями: х + 2у – 4 = 0, у = 0, х = -3, и х = 2

Выполним построение фигуры (см. рис.) Строим прямую х + 2у – 4 = 0 по двум точкам А(4;0) и В(0;2). Выразив у через х, получим у = -0,5х + 2. По формуле (1), где f(x) = -0,5х + 2, а = -3, в = 2, находим

S = = [-0,25=11,25 кв. ед

Пример 2. Вычислить площадь фигуры, ограниченной линиями: х – 2у + 4 = 0, х + у – 5 = 0 и у = 0.

Решение. Выполним построение фигуры.

Построим прямую х – 2у + 4 = 0: у = 0, х = - 4, А(-4; 0); х = 0, у = 2, В(0; 2).

Построим прямую х + у – 5 = 0: у = 0, х = 5, С(5; 0), х = 0, у = 5, D(0; 5).

Найдем точку пересечения прямых, решив систему уравнений:

х = 2, у = 3; М(2; 3).

Для вычисления искомой площади разобьем треугольник АМС на два треугольника АМN и NМС, так как при изменении х от А до N площадь ограничена прямой, а при изменении х от N до С - прямой

Для треугольника АМN имеем: ; у = 0,5х + 2, т. е. f(x) = 0,5х + 2, a = - 4, b = 2.

Для треугольника NМС имеем: y = - x + 5, т. е. f(x) = - x + 5, a = 2, b = 5.

Вычислив площадь каждого из треугольников и сложив результаты, находим:

кв. ед.

кв. ед.

9 + 4, 5 = 13,5 кв. ед. Проверка: = 0,5АС = 0,5 кв. ед.

Пример 3. Вычислить площадь фигуры, ограниченной линиями: y = x 2 , y = 0, x = 2, x = 3.

В данном случае требуется вычислить площадь криволинейной трапеции, ограниченной параболой y = x 2 , прямыми x = 2 и x = 3и осью Ох(см. рис.) По формуле (1) находим площадь криволинейной трапеции

= = 6кв. ед.

Пример 4. Вычислить площадь фигуры, ограниченной линиями: у = - x 2 + 4 и у = 0

Выполним построение фигуры. Искомая площадь заключена между параболой у = - x 2 + 4 и осью Ох.

Найдем точки пересечения параболы с осью Ох. Полагая у = 0, найдем х = Так как данная фигура симметрична относительно оси Оу, то вычислим площадь фигуры, расположенной справа от оси Оу, и полученный результат удвоим: = +4x]кв. ед. 2 = 2 кв. ед.

Пример 5. Вычислить площадь фигуры, ограниченной линиями: y 2 = x, yx = 1, x = 4

Здесь требуется вычислить площадь криволинейной трапеции, ограниченной верхней ветвью параболыy 2 = x, осью Ох и прямыми x = 1иx = 4 (см. рис.)

По формуле (1), где f(x) = a = 1 и b = 4 имеем = (= кв. ед.

Пример 6 . Вычислить площадь фигуры, ограниченной линиями:y = sinx, y = 0, x = 0, x= .

Искомая площадь ограничена полуволной синусоиды и осью Ох (см. рис.).

Имеем - cosx = - cos = 1 + 1 = 2 кв. ед.

Пример 7. Вычислить площадь фигуры, ограниченной линиями: y = - 6х, у = 0 и х = 4.

Фигура расположена под осью Ох (см. рис.).

Следовательно, её площадь находим по формуле (3)

= =

Пример 8. Вычислить площадь фигуры, ограниченной линиями:y = и х = 2. Кривую y = построим по точкам (см. рис.). Таким образом, площадь фигуры находим по формуле (4)

Пример 9 .

х 2 + у 2 = r 2 .

Здесь требуется вычислить площадь, ограниченную окружностью х 2 + у 2 = r 2 , т. е. площадь круга радиуса r с центром в начале координат. Найдем четвертую часть этой площади, взяв пределы интегрирования от 0

доr; имеем: 1 = = [

Следовательно, 1 =

Пример 10. Вычислить площадь фигуры, ограниченной линиями: у= х 2 и у = 2х

Данная фигура ограничена параболой у= х 2 и прямой у = 2х (см. рис.) Для определения точек пересечения заданных линий решим систему уравнений:х 2 – 2х = 0 х = 0 и х = 2

Используя для нахождения площади формулу (5), получим

= , в каждом из которых функция сохраняет знак.

По правилу знаков, на отрезке [π , 2π ] площадь берется со знаком минус.

В итоге, искомая площадь равна

Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг большой оси a .

Решение.

Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Ox площади OAB , равной одной четверти площади эллипса, и полученный результат удвоить.

Обозначим объем тела вращения через V x ; тогда на основании формулы имеем , где 0 и a - абсциссы точек B и A . Из уравнения эллипса находим . Отсюда

Таким образом, искомый объем равен . (При вращении эллипса вокруг малой оси b , объем тела равен )

Найти площадь, ограниченную параболами y 2 = 2 px и x 2 = 2 py .

Решение.

Сначала найдем координаты точек пересечения парабол, чтобы определить отрезок интегрирования. Преобразуя исходные уравнения, получаем и . Приравнивая эти значения, получим или x 4 - 8p 3 x = 0.

x 4 - 8p 3 x = x (x 3 - 8p 3) = x (x - 2p )(x 2 + 2px + 4p 2) = 0.

Находим корни уравнений:

Учитывая то факт, что точка A пересечения парабол находится в первой четверти, то пределы интегрирования x = 0 и x = 2p .

Искомую площадь находим по формуле

На этом уроке будем учиться вычислять площади плоских фигур , которые называются криволинейными трапециями .

Примеры таких фигур - на рисунке ниже.

С одной стороны, найти площадь плоской фигуры с помощью определённого интеграла предельно просто. Речь идёт о площади фигуры, которую сверху ограничивает некоторая кривая, снизу - ось абсцисс (Ox ), а слева и справа - некоторые прямые. Простота в том, что определённый интеграл функции, которой задана кривая, и есть площадь такой фигуры (криволинейной трапеции).

Для вычисления площади фигуры нам понадобятся:

Определённый интеграл от функции, задающей кривую , которая ограничивает криволинейную трапецию сверху. И здесь возникает первый существенный нюанс: криволинейная трапеция может быть ограничена кривой не только сверху, но и снизу . Как действовать в этом случае? Просто, но это важно запомнить: интеграл в этом случае берётся со знаком минус .

Пределы интегрирования a и b , которые находим из уравнений прямых, ограничивающих фигуру слева и справа: x = a , x = b , где a и b - числа.

Отдельно ещё о некоторых нюансах .

Кривая, которая ограничивает криволинейную трапецию сверху (или снизу) должна быть графиком непрерывной и неотрицательной функции y = f (x ) .

Значения "икса" должны принадлежать отрезку [a , b ] . То есть не учитываются такие, например, линии, как разрез гриба, у которого ножка вполне вписывается в этот отрезок, а шляпка намного шире.

Боковые отрезки могут вырождаться в точки . Если вы увидели такую фигуру на чертеже, это не должно вас смущать, так как эта точка всегда имеет своё значение на оси "иксов". А значит с пределами интегрирования всё в порядке.

Теперь можно переходить к формулам и вычислениям. Итак, площадь s криволинейной трапеции может быть вычислена по формуле

Если же f (x ) ≤ 0 (график функции расположен ниже оси Ox ), то площадь криволинейной трапеции может быть вычислена по формуле

Есть ещё случаи, когда и верхняя, и нижняя границы фигуры - функции, соответственно y = f (x ) и y = φ (x ) , то площадь такой фигуры вычисляется по формуле

. (3)

Решаем задачи вместе

Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).

Пример 1. Ox ) и прямыми x = 1 , x = 3 .

Решение. Так как y = 1/x > 0 на отрезке , то площадь криволинейной трапеции находим по формуле (1):

.

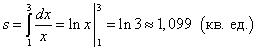Пример 2. Найти площадь фигуры, ограниченной графиком функции , прямой x = 1 и осью абсцисс (Ox ).

Решение. Результат применения формулы (1):

Если то s = 1/2 ; если то s = 1/3 , и т.д.

Пример 3. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox ) и прямой x = 4 .

Решение. Фигура, соответствующая условию задачи - криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку , по формуле (1) находим площадь криволинейной трапеции:

.

Пример 4. Найти площадь фигуры, ограниченной линиями , , и находящейся в 1-й четверти.

Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC . При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A , а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox ). Решая совместно (как систему) уравнения прямой и параболы, получим (абсциссу точки A ) и (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим , (абсциссы точек C и D ). Теперь у нас еть всё для нахождения площади фигуры. Находим:

Пример 5. Найти площадь криволинейной трапеции ACDB , если уравнение кривой CD и абсциссы A и B соответственно 1 и 2.

Решение. Выразим данное уравнение кривой через игрек: Площадь криволинейной трапеции находим по формуле (1):

.

Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).

Пример 6. Найти площадь фигуры, ограниченной параболой и осью абсцисс (Ox ).

Решение. Данная фигура расположена ниже оси абсцисс. Поэтому для вычисления её площади воспользуемся формулой (2). Пределами интегрирования являются абсциссы и точек пересечения параболы с осью Ox . Следовательно,

Пример 7. Найти площадь, заключённую между осью абсцисс (Ox ) и двумя соседними волнами синусоиды.

Решение. Площадь данной фигуры можем найти по формуле (2):

.

Найдём отдельно каждое слагаемое:

.

.

Окончательно находим площадь:

.

Пример 8. Найти площадь фигуры, заключённой между параболой и кривой .

Решение. Выразим уравнения линий через игрек:

Площадь по формуле (2) получим как

,

где a и b - абсциссы точек A и B . Найдём их, решая совместно уравнения:

Окончательно находим площадь:

И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3).

Пример 9. Найти площадь фигуры, заключённой между параболами и .

Пусть функция неотрицательна и непрерывна на отрезке . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямыми и (см. рис. 2) вычисляется по формуле

Пример 9. Найти площадь фигуры, ограниченной линией и осью .

Решение . Графиком функции является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (прямой ). Для этого решаем систему уравнений

Получаем: , откуда , ; следовательно, , .

Рис. 3

Площадь фигуры находим по формуле (5):

Если функция неположительна и непрерывна на отрезке , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , слева и справа – прямыми и , вычисляется по формуле

. (6)

В случае, если функция непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:

Рис. 4

Пример 10. Вычислить площадь фигуры, ограниченной осью и графиком функции при .

Рис. 5

Решение . Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей и . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему Получим , . Следовательно:

;

.

Таким образом, площадь заштрихованной фигуры равна

(кв. ед.).

Рис. 6

Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке функций и ,
а слева и справа – прямыми и (рис. 6). Тогда ее площадь вычисляется по формуле

. (8)

Пример 11. Найти площадь фигуры, ограниченной линиями и .

Решение. Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений находим , ; следовательно, , . На отрезке имеем: . Значит, в формуле (8) в качестве возьмем x , а в качестве – . Получим:

(кв. ед.).

Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.

Рис. 7

Пример 12. Найти площадь фигуры, ограниченной линиями , , .

Решение . Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью , слева и справа – прямыми и , сверху – графиками функций и . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой на две части (1 – это абсцисса точки пересечения линий и ). Площадь каждой из этих частей находим по формуле (4):

(кв. ед.); (кв. ед.). Следовательно:

(кв. ед.).

Рис. 8

х = j (у )

Рис. 9

В заключение отметим, что если криволинейная трапеция ограничена прямыми и , осью и непрерывной на кривой (рис. 9), то ее площадь находится по формуле

Объем тела вращения

Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке функции , осью , прямыми и , вращается вокруг оси (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле

. (9)

Пример 13. Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой , прямыми , и осью .

Решение . Сделаем чертеж (рис. 11).

Из условия задачи следует, что , . По формуле (9) получаем

.

Рис. 10

Рис. 11

Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d , осью Оу и графиком непрерывной на отрезке функции (рис. 12), определяется по формуле

. (10)

х = j (у )

Рис. 12

Пример 14 . Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х 2 = 4у , у = 4, х = 0 (рис. 13).

Решение . В соответствии с условием задачи находим пределы интегрирования: , . По формуле (10) получаем:

Рис. 13

Длина дуги плоской кривой

Пусть кривая , заданная уравнением , где , лежит в плоскости (рис. 14).

Рис. 14

Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.

Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле

. (11)

Пример 15 . Вычислить длину дуги кривой , заключенной между точками, для которых .

Решение . Из условия задачи имеем . По формуле (11) получаем:

.

4. Несобственные интегралы
с бесконечными пределами интегрирования

При введении понятия определённого интеграла предполага-лось, что выполняются следующие два условия:

а) пределы интегрирования а и являются конечными;

б) подынтегральная функция ограничена на отрезке .

Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным .

Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.

Определение. Пусть функция определена и непрерывна на промежутке , тогда и неограниченной справа (рис. 15).

Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.

Рис. 15

Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:

. (13)

Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.

Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:

, (14)

где с – любая точка интервала . Интеграл сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).

;

г) = [выделим в знаменателе полный квадрат: ] = [замена:

] =

Значит, несобственный интеграл сходится и его значение равно .