Что такое пропорциональное деление. Составление системы уравнений
{module Адаптивный блок Адсенс в начале статьи}
ЗАДАЧИ НА ПРОПОРЦИОНАЛЬНОЕ ДЕЛЕНИЕ
4 КЛАСС
Задачи на пропорциональное деление получили свое название по способу их решения. Чтобы дать ответ на вопрос задачи необходимо составить некоторую пропорцию и рассчитать как соотносятся между собой искомые величины.
Рассмотрим решение задачи на пропорциональное деление на примере:
Задача: Двое рабочих заработали 9000 рублей. Один работал 2 недели, а другой 8 недель. Сколько денег заработал каждый?
Решение: Исходя из условия задачи, можно найти как оплачивается одна неделя такой работы:
9000 ÷ (8 + 2) = 900 рублей за неделю.
900 · 2 = 1800 рублей - один рабочий;
900 · 8 = 7200 рублей - другой рабочий.
Ответ: 1800 и 7200.
Примеры задач на пропорциональное деление:
1) Двое рабочих получили 8000 рублей. Как они разделят свой заработок, если один работал 6 недель, а другой 4 недели?
2) 25 м проволоки весят 700 г. Взяли два мотка проволоки. В одном мотке 30 м проволоки, а в другом на 15 м больше. Сколько весит каждый моток?
3) Для приготовления торфоперегнойных горшков берут на 7 частей земли 2 части торфа. Сколько нужно взять земли на 200 кг торфа?
4) Две школы выписали на 960 рублей клубничной рассады. Одна школа взяла 3 ящика, а другая 5 ящиков. Сколько должна заплатить каждая школа за рассаду клубники?
5) Два грузовика перевезли 77 т груза, сделав одинаковое число рейсов. Сколько тонн груза перевёз каждый грузовик, если один грузовик перевозил за рейс 3 т, а другой - 4 т?
6) Двое рабочих выписали из питомника 26 яблонь. Как они должны разделить яблони, если один дал на покупку 500 рублей, а другой 800 рублей?
7) Сколько граммов резинового клея получится из 50 г каучука, если для приготовления клея берут на одну часть каучука 9 частей очищенного бензина?
8) Двое рабочих заработали 8400 рублей. Первый работал 5 недель, а второй 7 недель. Сколько денег заработал каждый рабочий?
9) Две бригады работали одинаковое время и заработали вместе 810 рублей. Как они должны разделить этот заработок, если в одной бригаде было 4 человека, а в другой 5?
10) Клуб купил одинаковое число лыж и коньков. Пара коньков стоит 6 долларов, а пара лыж 9 долларов. Сколько стоят отдельно коньки и лыжи, если за всю покупку заплатили 900 долларов?
11) Для приготовления жидкого столярного клея берут 15 частей плиточного клея и 17 частей воды. Сколько нужно взять плиточного клея для изготовления 640 г жидкого столярного клея?
12) На 118 рублей купили одинаковое число пальто для мальчиков и девочек. Сколько куплено тех и других, если каждое пальто для мальчиков стоило 31 марку, а для девочек 28 марок?
13) Колхоз привёз одинаковое количество ящиков яблок и груш. Каждый ящик груш весил 50 кг, а ящик яблок 40 кг. Все фрукты вместе весили 810 кг. Сколько килограммов тех и других фруктов отдельно привезли?
14) В двух кусках 24 м сукна. Один кусок стоит 240 долларов, а другой 480 долларов. Сколько метров сукна в каждом куске?
15) "Москвич" на 100 км пути расходует 9 л бензина, "Волга" - 13 л. Обеим машинам отпущено 66 л бензина на 300 км пути. Сколько литров бензина отпущено каждой машине?
{module Адаптивный блок Адсенс в конце статьи}
Тема урока : Пропорциональное деление
В школьном курсе математики предлагается очень мало задач на «пропорциональное деление». Однако их можно встретить в экзаменационных сборниках для 9 класса авт. Л.И.Звавич и др. Эти задачи предлагаются на вступительных экзаменах в ВУЗы на специальности, связанные с экономикой, химией, связанных с легкой промышленностью и народного хозяйства.
Предлагаемые задачи можно использовать на факультативах в общеобразовательных школах, включить их в программу гимназий и лицеев, связанных с углубленным изучением математики, начиная с 6 класса, для индивидуальной работы с сильными учениками.
Эти задачи может решить шестиклассник.
Необходимость разделить заданную величину или число в данном отношении часто возникает в практической жизни человека – при приготовлении различных смесей, растворов, блюд по кулинарным рецептам, при распределении прибыли или мест в парламенте и так далее.
Например, если два предпринимателя вложили в проект соответственно 3 млн. рублей и 4 млн.рублей и получили 14 млн. рублей прибыли, то справедливость требует, чтобы полученная прибыль делилась пропорционально
числам 3 и 4. Само слово «пропорционально» происходит от латинского «гармонично», «соразмерно».
Как же узнать, сколько денег должен получить каждый предприниматель? Обозначим части, которые они должны получить, соответственно a и b. Тогда a: b = 3: 4.
Поменяем в пропорции местами средние члены и обозначим коэффициент пропорциональности k. Получим равенство:
Из которого следует, что а = 3k, b = 4k. Так как сумма двух частей составляет 14 млн. рублей, то значение k должно удовлетворять равенству
3k + 4k =14 <=> 7k = 14 <=> k = 2.
Значит, при справедливом делении первый предприниматель должен получить 2 3 = 6 млн.рублей, а второй - 2 4 = 8 млн.рублей.
Рассмотрим еще одну задачу.
Для приготовления строительного раствора на 2 части цемента берут 2 части песка и 0,8 частей воды. Сколько цемента, песка и воды потребуется для приготовления 180 кг раствора?
Решение:
1) Пусть для приготовления строительного раствора требуется а кг цемента, b кг песка и с кг воды. Обозначим коэффициент пропорциональности k , тогда
Следовательно, а = 2 k , b = 2 k , c = 0,8 k .
По условию задачи, сумма всех частей равна 180 кг, значит:
2 k + 2 k + 0,8 k = 180 <=>4,8 k = 180 <=> k = 37,5.
2) 37,5 2 = 75 (кг) – потребуется песка и цемента.
3) 37,5 0,8 = 30 (кг) – потребуется воды.
Ответ: потребуется 75 кг цемента, 75 кг песка и 30 кг воды.
Для краткого обозначения условия задач о прямо пропорциональном делении в математическом языке используют иногда «длинные отношения». Например, a: b: c = 2: 2: 0,8.
При этом говорят: «Числа a, b и с относятся как 2 к 3 к 0,8».
Длинные отношения – это условные записи, которые показывают, сколько равных долей величины приходится на каждую часть. Их нельзя понимать как запись деления нескольких чисел. Действительно, подставив в последнее равенство вместо букв соответствующие им числа, получим верное высказывание
75: 75: 30 = 2: 2: 0,8;
Тогда как при непосредственном подсчете левой и правой части получаются разные числа: в левой части , а в правой части – 1,25.
Зато длинные отношения можно преобразовывать, как обычные дроби: умножать все его члены на одно и то же число, сокращать. Эти преобразования позволяют упрощать запись, а значит, и решение задач. Так, если бы в нашей задаче мы сначала умножили все члены отношения на 10, а затем разделили их на 4, то избавились бы от дробей:
2: 2: 0,8 = 20: 20: 8 = 5: 5: 2
и получили более простое уравнение.
Решая задачи на пропорциональное деление, мы вновь наблюдаем, как абстрактные математические понятия – в данном случае прямая и обратная пропорциональность – помогают отвечать на серьезные практические вопросы.
Предлагаю еще несколько задач по этой теме.
Задача 1.
Трое рабочих получили 4080 рублей. Суммы, полученные первым и вторым рабочими, относятся, как . Сумма, полученная третьим рабочим составляет того. Что получил первый рабочий. Сколько денег получил каждый рабочий?
Решение:
Ответ: 2448 рублей получил первый рабочий; 571,2 рубля получил второй рабочий и 1060,8 рубля получил третий рабочий.
Задача 2.
Три цеха сшили 16800 пар обуви. Количество пар обуви сшитой первым и вторым цехами относятся как а третий цех сшил 75% того, что сшил первый цех. На сколько процентов выполнил план первый цех, если план каждого цеха был 4000 пар обуви?
Решение:
Ответ: на 180% выполнил план первый цех.
Задача 3.
В палатку привезли свеклу, морковь, капусту. Количество свеклы и моркови равно отношению , а вес капусты составляет 250% от веса моркови. Капусты было на 80 кг больше, чем свеклы. Сколько килограммов каждого овоща привезли в палатку?
Решение:
Ответ: в палатку привезли 120 кг свеклы; 80 кг моркови и 200 кг капусты.
Задача 4.
Магазин продал за 4 дня некоторое количество ткани. Количество ткани, проданной за первые три дня относились, как 0,9: 1,4: 1,3. В четвертый день продали 420 м ткани, что составило 28% всей ткани, проданной магазином за четыре дня. Сколько ткани продали за каждый день?
Решение:
- n1 : n2 : n3 = 0,9: 1,4: 1,3 = 9: 14: 13
- 28% составляет 420 м: 420: 0,28 = 1500 (м) – ткани продали за четыре дня.
- 1500 – 420 = 1080 (м) – ткани продали за первые три дня.
- 9 + 14 + 13 = 36 (ч.) – приходится на 1080 м ткани.
- 1080: 36 = 30 (м) – ткани приходится на 1 часть.
- 30 9 = 270 (м) – ткани продали за первый день.
- 30 14 = 520 (м) – ткани продали за второй день.
- 30 13 = 390 (м) – ткани продали за третий день.
Ответ: магазин продал 270 м ткани за первый день; 520 м ткани за второй день; 390 м ткани за третий день и 420 м за четвертый день.
Задача 5.
Три класса собирали металлолом. Количество металлолома, собранного первым и вторым классами относится, как 4,5: 3. Количество металлолома, собранного третьим классом составляет 40% того, что собрал первый класс. Сколько металлолома собрал каждый класс, если второй класс собрал на 0,8 тонны металлолома больше, чем третий класс?
Решение:
- n1 : n2 = 4,5: 3 = 45: 30 = 3: 2.
- 40% от 3: 3 0,4 = 1,2(ч.) – приходится на третий класс
- n1 : n2 : n3 = 3: 2: 1,2 = 30: 20: 12 =15: 10: 6.
- 10 – 6 = 4 (ч.) – приходится на 0,8 т металлолома.
- 0,8: 4 15 = 3 (т) – собрал первый класс.
- 0,8: 4 10 = 2 (т) – собрал второй класс.
- 0,8: 4 6 = 1,2 (т) – собрал третий класс.
Ответ: первый класс собрал 3 т металлолома, второй класс собрал
2 т металлолома, третий класс собрал 1,2 т металлолома.
Задача 6.
Три бригады начали одновременно пахоту земли. Норма вспашки первой бригады ко второй относится как 0,5 к 0,4, а норма вспашки второй бригады к третьей относится как 2 к 1,8; но первая и третья бригады увеличили нормы вспашки на 10%, а вторая бригада – на 20%. Таким образом, к одному и тому же сроку,первая бригада вспахала на 15,4 га больше, чем третья бригада. Сколько га земли вспахала к этому времени каждая бригада?
Решение:
- n1 : n2 = 0,5: 0,4 = 5: 4.
- n2 : n3 = 2: 1,8 = 20 = 18 = 10: 9
- выразим n 1 : n 2 : n 3 в одинаковых долях n 1 : n 2 : n 3 =25: 20: 18
- 10% от 25: 25 0,1 = 2,5; 25 + 2,5 = 27,5 (ч) составляет норма первой бригады после увеличения.
- 20% от 20: 20 0,2 = 4 ; 20 + 4 = 24 (ч) –составляет норма второй бригады после увеличения.
- 10% от 18: 18 0,1 = 1,8; 18 + 1,8 = 19,8 (ч) составляет норма третьей бригады после увеличения.
- n 1 : n 2 : n 3 =27,5: 24: 19,8 = 275: 240: 198
- 275 – 198 – 77(ч) – приходится на 14, 4 га земли
- 15,4: 77 = 0,2 (га) – приходится на одну часть.
- 0,2 275 = 55 (га) – вспахала первая бригада.
- 0,2 240 = 48(га) – вспахала вторая бригада.
- 0,2 198 = 39,6 (га) – вспахала третья бригада.
Ответ: 55 га земли вспахала первая бригада, 48 га земли спахала вторая бригада, 39,6 га земли вспахала третья бригада.
Предлагаю несколько задач для самостоятельного решения.
Задача 1.
Колхоз засыпал в три склада картофель в отношении 1,3 к 2,5 к 1,2, причем во второй склад засыпали на 43,2 тонны картофеля больше, чем в первый склад. В течение месяца с первого склада вывезли 40% имевшегося там картофеля, со второго - 30%, а с третьего – 25% имевшегося там картофеля. Сколько картофеля вывезли с трех складов?
Ответ: вывезли всего 56,62 т картофеля.
Задача 2.
Магазин продавал муку в течение четырех дней. Количество муки, проданной за первые три дня, относится, как 1,8 к 2,8 к 2,6. В четвертый день продали 840 килограммов муки, что составляет 56% всей муки, проданной за четыре дня. Сколько муки продавали каждый день?
Задача 3.
Колхоз засыпал зерно в три склада. На первом складе было 40% всего зерна, засыпанного в три склада. Количество зерна, засыпанного во второй и третий склады, относится, как 16 к 21. Сколько зерна было на первом складе, если на третьем складе было на 450 ц больше, чем на втором.
Ответ: 2220 ц зерна было засыпано в первый склад.
Задача 4.
Три цеха изготовили 6500 деталей. Количество деталей, изготовленных первым и вторым цехами, относится, как 0,1875 к 0,25., количество деталей, изготовленных третьим цехом на 50% больше, чем количество деталей, изготовленных вторым цехом.. Сколько деталей изготовил каждый цех.
Задача 5.
Отряд отправился в поход из пункта А в пункт В. Первую часть пути школьники проехали на велосипедах, вторую часть пути прошли пешком, а оставшиеся 30 километров проплыли на лодке. Зная, что длины этих частей пути относятся, как 1,625 к 1,3 к 3, 25, определите длину всего маршрута.
Ответ: длина всего маршрута 57 километров.
Задача 6.
Из четырех чисел первые три относятся между собой, как , а четвертое составляет 40% от первого числа. Найти сумму всех четырех чисел, если первое больше суммы остальных на 40.
Продолжим решение задач.
Задача 7.
Найти сумму трех чисел, зная, что первое число равно 100, а первое число относится ко второму, как ; а второе к третьему, как 12 к 7.
Решение:
Ответ: сумма трех чисел равна 385.
Задача 8.
Найти сумму трех чисел, зная, что первое число относится к третьему, как
; второе число относится к третьему как 5 к 2, а сумма первых двух чисел равна 500.
Решение:
Ответ: сумма трех чисел равна 650.
Задача 9.
Найти каждое из трех чисел, если первое число относится ко второму как 0,6: 0,75, а второе к третьему, как 1: 0,9. Сумма первого и третьего чисел на 105 больше второго числа.
Решение:
- n 1 : n 3 = 0,6: 0,75 = 60: 75 = 4: 5
- n 2 : n 3 = 1: 0,9 = 10: 9.
- выразим n 1 : n 2 : n 3 в одинаковых долях n 1 : n 2 : n 3 = 8: 10: 9.
- (8 + 9) – 10 = 7 (ч.) – приходится на 105.
- 105: 7 8 = 120 – первое число.
- 105: 7 10 – 150 – второе число.
- 105: 7 9 = 135 – третье число.
Ответ: 120; 150; 135.
Задача 10.
Из данных четырех чисел первые три относятся, как , а четвертое составляет 15% второго числа. Найти эти числа, если известно, что второе число больше суммы остальных на 8.
Решение:
Ответ: 48; 80; 12; 12.
Задача 11.

Задача 12.
Три колхоза построили хлебозавод. Суммы, внесенные колхозами в строительство, относятся, как . Сколько денег внес каждый колхоз, если стройматериалы стоят 1620 миллионов рублей, расход на рабочую силу составляет от стоимости материала, на оборудование израсходовали стоимости материала и рабочей силы вместе?
Решение:
Ответ: на материалы – 2700 млн.рублей; на рабочую силу – 3600 млн.рублей; на оборудование – 4500 млн. рублей.
Методика обучения решению задач на нахождения четвертого пропорционального.
Задача на нахождение четвертого пропорционального – это задача, в которой даны три величины, связанные прямо или обратно пропорциональной зависимостью, из них две переменные и одна постоянная, при этом известны два значения одной переменной величины и одно из соответствующих значений другой переменной величины, а второе значение этой величины является искомым.
Особое внимание необходимо уделить классификации задач на нахождение четвертого пропорционального. Используя любые три величины, связанные пропорциональной зависимостью (третья равна произведению первой и второй), можно составить шесть видов задач на нахождение четвертого пропорционального. Среди этих задач первые четыре задачи с прямо пропорциональной зависимостью величин, а две последние с обратно пропорциональной.
Основным способом решения задач такого вида в начальной школе – арифметический (нахождение значения постоянной величины и нахождением отношения двух значений одной величины), также практикуется и алгебраический способ решения (уравнением).
Для решения задачи удобно записывать данные условия в виде таблицы.
Этапы обучения решению задач на нахождение четвертого пропорционального аналогичны как и в работе с другими задачами – подготовительный, ознакомительный, закрепление. В начале рассматривают преимущественно задачи с прямо пропорциональной зависимостью с такими группами величин:
Цена, количество, стоимость;
Масса одного предмета, число предметов, общая масса;
Емкость одного сосуда, число сосудов, общая емкость;
Выработка (производительность) в единицу времени, время работы, общая выработка;
Расход материи на одну вещь, число вещей, общий расход материи. Далее вводятся новые группы величин: скорость, время, расстояние; длина прямоугольника, его ширина и площадь; урожай с единицы площади, площадь и весь урожай. В это время уже рассматриваются задачи всех шести видов.
Задача на пропорциональное деление включает три величины, связанные пропорциональной зависимостью, из них две переменные и одна или больше постоянных, причем даны два или более значений одной переменной и сумма соответствующих значений другой переменной, слагаемые этой суммы являются искомыми.
В НШ решаются задачи только на пропорциональное деление только с прямо пропорциональной зависимостью величин, решаются только способом нахождения значения постоянной величины.
Подготовкой к решению задач на пропорциональное деление является твердое умение школьников решать задачи на нахождение четвертого пропорционального.
При ознакомлении с задачами на пропорциональное деление следует получить задачи этого вида путем совместной с учащимися работы по преобразованию задач на нахождение четвертого пропорционального в задачи нового вида. Или составление задачи по записанной таблице. Таким образом, необходимо отметить важность наличия у детей сформированного умения составлять и преобразовывать задачи.
Для решения задачи удобно записывать данные условия в виде таблицы. Следует обратить особое внимание на особенности работы с ознакомлением данного вида задач поэтапно.
В начале рассматривают преимущественно задачи на пропорциональное деление первого вида с такими группами величин: цена, количество, стоимость; масса одного предмета, число предметов, общая масса; емкость одного сосуда, число сосудов, общая емкость и др. После этого вводятся задачи второго вида, а несколько позднее третьего и четвертого видов. Следует отметить, что в начальной школе в основном решаются задачи с прямо пропорциональной зависимостью величин.
При первоначальном ознакомлении применять чертеж нецелесообразно, т.к. учащиеся усваивают формальные рассуждения, т.е. происходит преждевременное сокращение рассуждений. Разбор задачи изображать в виде графической схемы тоже нецелесообразно, т.к. она начнется с двух вопросов и вызывает затруднение учащихся.
Для закрепления решения задач на пропорциональное деление в дальнейшем включаются задачи с другими величинами и другие задачи из этой группы. Используются упражнения творческого характера на составление и преобразование задач.
Пропорциональное деление
деление какой-либо величины в данном отношении. Если данная величина есть a
, a отношение есть n
, то надо разделить a
на две части x
и (а-х
) так, чтобы отношение x
к (a-x
) равнялось бы n.
Выразив это уравнением и решив его относительно x
, получим: x
= an
/(1 + n
). К числу вопросов о пропорциональном делении относятся две известные геометрические задачи: найти длину x
, среднепропорциональную двум данным длинам a
и b
; разделить данную длину в крайнем и среднем отношении. Построения, с помощью которых получаются решения этих и подобных задач, приводятся в начальных учебниках геометрии.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. - С.-Пб.: Брокгауз-Ефрон . 1890-1907 .
Смотреть что такое "Пропорциональное деление" в других словарях:
Правило товарищества, арифметич. способ деления числа на части, пропорциональные данным числам; находит частое применение при делении прибыли между товарищами пропорционально (соответственно) внесенным ими в предприятие капиталам или… …
- (лат. proportionalis от proportio отношение, сходство, пропорция). Соразмерный, правомерный. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНЫЙ лат. propotiornalis, от proportio, пропорция.… … Словарь иностранных слов русского языка
ПРОПОРЦИОНАЛЬНЫЙ, пропорциональная, пропорциональное; пропорционален, пропорциональна, пропорционально (лат. proporcionalis соразмерный) (книжн.). 1. Обладающий соразмерностью частей. Пропорциональное телосложение. 2. Такой, который с увеличением … Толковый словарь Ушакова
История науки … Википедия
Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике … Википедия
Данная статья часть обзора История математики. Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II… … Википедия
История науки По тематике Математика Естественные науки … Википедия
Петров (Иван) русский феноменальный счетчик. Родился в 1823 году в крестьянской крепостной семье в Костромской губернии. В раннем возрасте, не умея ни читать, ни писать, он поражал окружающих своими способностями к счету и решению задач. В… … Биографический словарь
Русский феноменальный счетчик. Родился в 1823 г. в крестьянской крепостной семье, Костромской губернии. В раннем возрасте, не умея ни читать, ни писать, он поражал окружающих своими способностями к счету и решению задач. В возрасте 11 лет… …
Феноменальный счетчик, родился в 1823 году в дер. Рагозино Кологривского у. Костромской губ.; родители его были крепостными крестьянами помещицы Волтатис. Несмотря на свою неграмотность, П. еще в самом раннем возрасте поражал своими способностями … Большая биографическая энциклопедия
Книги
- Арифметика: Целые числа. О делимости чисел. Измерение величин. Метрическая система мер. Обыкновенные , Киселев, Андрей Петрович. Вниманию читателей предлагается книга выдающегося отечественного педагога и математика А. П. Киселева (1852-1940), содержащая систематический курс арифметики. Книга включает шесть разделов.…
- Арифметика , Киселев А.. Целые числа. О делимости чисел. Измерения величин. Метрическая система мер. Обыкновенные (простые) дроби. Десятичные дроби. Пропорциональные величины. Вниманиючитателей…
- Арифметика. Целые числа. О делимости чисел. Измерение величин. Метрическая система мер. Обыкновенные (простые) дроби. Десятичные дроби. Пропорциональные величины , Киселев А.П.. Вниманию читателей предлагается книга выдающегося отечественного педагога и математика А. П. Киселева (1852-1940), содержащая систематический курс арифметики. Книга включает шесть разделов.…
В основе задач на пропорциональное деление лежат задачи на нахождение четвертого пропорционально. Поэтому к задачам на пропорциональное деление приступают после ознакомления с задачами на нахождение четвертого пропорционального.
К задачам на пропорциональное деление относятся следующие:
а). задачи на части или задачи, решаемые делением пропорционально ряду данных чисел;
б). Задачи на нахождение чисел по сумме и кратному отношению;
в). задачи, решаемые делением числа пропорционально нескольким рядам чисел.
Остановимся на рассмотрении задач первого типа.
"За два куска одинаковой ткани в 5 м и 7 м заплатили 36 рублей.. Сколько стоит каждый кусок ткани?"
Составим таблицу:
Устанавливая зависимость между данными и искомыми, обращаем внимание на то, что если ткань одна и та же, то ее цена одинакова и поэтому, чем больше метров в куске такой ткани, тем он дороже. Следовательно, второй кусок дороже первого. Однако сразу найти стоимость какого-либо куска ткани нельзя, так как не указана цена.
Чтобы узнать цену, нужно знать общую стоимость всей ткани - в условиях она указана – и общее число метров ткани в двух кусках. Это число можно найти, так как известны размеры первого и второго кусков. На основе этого анализа составляем план решения:
Найдем число метров ткани в двух кусках.
Узнаем цену 1 м ткани.
Вычислим стоимость первого куска ткани.
Вычислим стоимость второго куска ткани.
|
1). 5+7=12 (м) 2).36:12=3 (руб.) 3).3*5= 15 (руб.) 4).3*7=21 (руб.) |
12 м ткани стоят 36 руб. 3 руб. стоит 1 м ткани 15 руб. стоит первый кусок ткани. 21 руб. стоит второй кусок ткани |
Проверка решения задачи: 15+21 = 36. Стоимость всей ткани, полученная при решении, совпадает с числом, данным в условии.
Для проверки решения такой задачи можно использовать составление и решение обратной задачи. Следует иметь в виду, что обратная задача должна быть также задачей на пропорциональное деление.
§ 3. Задачи на нахождение чисел по двум разностям.
По степени сложности задачи на нахождение чисел по двум разностям относятся в разряд, следующий за задачами на пропорциональное деление. При решении задач указанного типа проводится сопоставление двух разностей, например разности в числе предметов и разности их стоимостей. Например:
“Мальчик купил 7 листов, а девочка 11 листов. Девочка заплатила на 12 коп. больше мальчика. Сколько заплатила за бумагу девочка и сколько мальчик?”
Краткий анализ условия и вопроса задачи позволит записать ее в виде таблицы:
Решая эту задачу, можно пойти по такому пути:
1) узнать, на сколько листов бумаги девочка купила больше, чем мальчик (11-7=4);
2). узнать цену листа бумаги (12:4=3);
3). найти, сколько заплатил за 7 листов мальчик (3*7=21);
4). сколько заплатила за 11 листов девочка (3*11=33).
При проверке узнают, на сколько копеек девочка заплатила больше, чем мальчик: 33-21=12, что совпадает с данным из условия.
Или составляют задачу, обратную данной. Обратная задача должна быть задачей того же типа.
 Могильники Чернобыля: радиоактивные отходы зоны отчуждения Где находится техника чернобыля
Могильники Чернобыля: радиоактивные отходы зоны отчуждения Где находится техника чернобыля Девочка заговорила на иностранном языке после комы
Девочка заговорила на иностранном языке после комы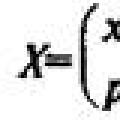 Сравнение законов распределения вероятностей
Сравнение законов распределения вероятностей