Значение экстремума. Как найти точки экстремума функции по графику производной. Введение в экстремумы функций

Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.

Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.

Yandex.RTB R-A-339285-1 Определение 1

Функция y = f (x) будет возрастать на интервале x , когда при любых x 1 ∈ X и x 2 ∈ X , x 2 > x 1 неравенство f (x 2) > f (x 1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.

Определение 2

Функция y = f (x) считается убывающей на интервале x , когда при любых x 1 ∈ X , x 2 ∈ X , x 2 > x 1 равенство f (x 2) > f (x 1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a ; b) , где х = а, х = b , точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x .

Основные свойства элементарных функций типа y = sin x – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале - π 2 ; π 2 , тогда возрастание на отрезке имеет вид - π 2 ; π 2 .

Определение 3

Точка х 0 называется точкой максимума для функции y = f (x) , когда для всех значений x неравенство f (x 0) ≥ f (x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается y m a x .

Точка х 0 называется точкой минимума для функции y = f (x) , когда для всех значений x неравенство f (x 0) ≤ f (x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида y m i n .

Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [ a ; b ] . Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х = b .

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Первое достаточное условие экстремума

Определение 4

Пусть задана функция y = f (x) , которая дифференцируема в ε окрестности точки x 0 , причем имеет непрерывность в заданной точке x 0 . Отсюда получаем, что

• когда f " (x) > 0 с x ∈ (x 0 - ε ; x 0) и f " (x) < 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• когда f " (x) < 0 с x ∈ (x 0 - ε ; x 0) и f " (x) > 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой минимума.

Иначе говоря, получим их условия постановки знака:

• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком, то есть с + на - , значит, точка называется максимумом;
• когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком с - на + , значит, точка называется минимумом.

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

• найти область определения;
• найти производную функции на этой области;
• определить нули и точки, где функция не существует;
• определение знака производной на интервалах;
• выбрать точки, где функция меняет знак.

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Пример 1

Найти точки максимума и минимума заданной функции y = 2 (x + 1) 2 x - 2 .

Решение

Область определения данной функции – это все действительные числа кроме х = 2 . Для начала найдем производную функции и получим:

y " = 2 x + 1 2 x - 2 " = 2 · x + 1 2 " · (x - 2) - (x + 1) 2 · (x - 2) " (x - 2) 2 = = 2 · 2 · (x + 1) · (x + 1) " · (x - 2) - (x + 1) 2 · 1 (x - 2) 2 = 2 · 2 · (x + 1) · (x - 2) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Отсюда видим, что нули функции – это х = - 1 , х = 5 , х = 2 , то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х = - 2 , х = 0 , х = 3 , х = 6 .

Получаем, что

y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0 , значит, интервал - ∞ ; - 1 имеет положительную производную. Аналогичным образом получаем, что

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2 < 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Получим, что в точке х = - 1 функция будет непрерывна, значит, производная изменит знак с + на - . По первому признаку имеем, что х = - 1 является точкой максимума, значит получаем

y m a x = y (- 1) = 2 · (x + 1) 2 x - 2 x = - 1 = 2 · (- 1 + 1) 2 - 1 - 2 = 0

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

y m i n = y (5) = 2 · (x + 1) 2 x - 2 x = 5 = 2 · (5 + 1) 2 5 - 2 = 24

Графическое изображение

Ответ: y m a x = y (- 1) = 0 , y m i n = y (5) = 24 .

Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x 0 , этим и упрощает вычисление.

Пример 2

Найти точки максимума и минимума функции y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 .

Решение.

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x < 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

После чего необходимо найти производную:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x < 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x > 0 y " = - 1 2 x 2 - 4 x - 22 3 , x < 0 1 2 x 2 - 4 x + 22 3 , x > 0

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

lim y " x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 · (0 - 0) 2 - 4 · (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 · (0 + 0) 2 - 4 · (0 + 0) + 22 3 = + 22 3

Отсюда следует, что функция непрерывна в точке х = 0 , тогда вычисляем

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 · (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 · (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 · 0 2 + 22 3 · 0 - 8 = - 8

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

1 2 x 2 - 4 x - 22 3 , x < 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 · 1 2 = 4 - 2 3 3 > 0

Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 . Получим, что

y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3 < 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 > 0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6 < 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 > 0 y " (4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 · 4 2 - 4 · 4 + 22 3 = - 2 3 < 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Изображение на прямой имеет вид

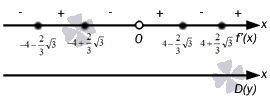
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , тогда отсюда точки максимума имеют значени x = - 4 + 2 3 3 , x = 4 - 2 3 3

Перейдем к вычислению минимумов:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Произведем вычисления максимумов функции. Получим, что

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Графическое изображение

Ответ:

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 8 27 3

Если задана функция f " (x 0) = 0 , тогда при ее f "" (x 0) > 0 получаем, что x 0 является точкой минимума, если f "" (x 0) < 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Пример 3

Найти максимумы и минимумы функции y = 8 x x + 1 .

Решение

Для начала находим область определения. Получаем, что

D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Необходимо продифференцировать функцию, после чего получим

y " = 8 x x + 1 " = 8 · x " · (x + 1) - x · (x + 1) " (x + 1) 2 = = 8 · 1 2 x · (x + 1) - x · 1 (x + 1) 2 = 4 · x + 1 - 2 x (x + 1) 2 · x = 4 · - x + 1 (x + 1) 2 · x

При х = 1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х = 1 . Получаем:

y "" = 4 · - x + 1 (x + 1) 2 · x " = = 4 · (- x + 1) " · (x + 1) 2 · x - (- x + 1) · x + 1 2 · x " (x + 1) 4 · x = = 4 · (- 1) · (x + 1) 2 · x - (- x + 1) · x + 1 2 " · x + (x + 1) 2 · x " (x + 1) 4 · x = = 4 · - (x + 1) 2 x - (- x + 1) · 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 · x = = - (x + 1) 2 x - (- x + 1) · x + 1 · 2 x + x + 1 2 x (x + 1) 4 · x = = 2 · 3 x 2 - 6 x - 1 x + 1 3 · x 3 ⇒ y "" (1) = 2 · 3 · 1 2 - 6 · 1 - 1 (1 + 1) 3 · (1) 3 = 2 · - 4 8 = - 1 < 0

Значит, использовав 2 достаточное условие экстремума, получаем, что х = 1 является точкой максимума. Иначе запись имеет вид y m a x = y (1) = 8 1 1 + 1 = 4 .

Графическое изображение

Ответ: y m a x = y (1) = 4 ..

Определение 5

Функция y = f (x) имеет ее производную до n -го порядка в ε окрестности заданной точки x 0 и производную до n + 1 -го порядка в точке x 0 . Тогда f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Отсюда следует, что когда n является четным числом, то x 0 считается точкой перегиба, когда n является нечетным числом, то x 0 точка экстремума, причем f (n + 1) (x 0) > 0 , тогда x 0 является точкой минимума, f (n + 1) (x 0) < 0 , тогда x 0 является точкой максимума.

Пример 4

Найти точки максимума и минимума функции y y = 1 16 (x + 1) 3 (x - 3) 4 .

Решение

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Данная производная обратится в ноль при x 1 = - 1 , x 2 = 5 7 , x 3 = 3 . То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401 < 0 y "" (3) = 0

Значит, что x 2 = 5 7 является точкой максимума. Применив 3 достаточный признак, получаем, что при n = 1 и f (n + 1) 5 7 < 0 .

Необходимо определить характер точек x 1 = - 1 , x 3 = 3 . Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Значит, x 1 = - 1 является точкой перегиба функции, так как при n = 2 и f (n + 1) (- 1) ≠ 0 . Необходимо исследовать точку x 3 = 3 . Для этого находим 4 производную и производим вычисления в этой точке:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) (3) = 96 > 0

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Графическое изображение

Ответ: x 2 = 5 7 является точкой максимума, x 3 = 3 - точкой минимума заданной функции.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Точка экстремума функции - это точка области определения функции , в которой значение функции принимает минимальное или максимальное значение. Значения функции в этих точках называются экстремумами (минимумом и максимумом) функции .

Определение . Точка x 1 области определения функции f (x ) называется точкой максимума функции , если значение функции в этой точке больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f (x 0 ) > f (x 0 + Δx ) x 1 максимум.

Определение . Точка x 2 области определения функции f (x ) называется точкой минимума функции , если значение функции в этой точке меньше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f (x 0 ) < f (x 0 + Δx ) ). В этом случае говорят, что функция имеет в точке x 2 минимум.

Допустим, точка x 1 - точка максимума функции f (x ) . Тогда в интервале до x 1 функция возрастает , поэтому производная функции больше нуля (f "(x ) > 0 ), а в интервале после x 1 функция убывает, следовательно, и производная функции меньше нуля (f "(x ) < 0 ). Тогда в точке x 1

Допустим также, что точка x 2 - точка минимума функции f (x ) . Тогда в интервале до x 2 функция убывает, а производная функции меньше нуля (f "(x ) < 0 ), а в интервале после x 2 функция возрастает, а производная функции больше нуля (f "(x ) > 0 ). В этом случае также в точке x 2 производная функции равна нулю или не существует.

Теорема Ферма (необходимый признак существования экстремума функции) . Если точка x 0 - точка экстремума функции f (x ) , то в этой точке производная функции равна нулю (f "(x ) = 0 ) или не существует.

Определение . Точки, в которых производная функции равна нулю или не существует, называются критическими точками .

Пример 1. Рассмотрим функцию .

В точке x = 0 производная функции равна нулю, следовательно, точка x = 0 является критической точкой. Однако, как видно на графике функции, она возрастает во всей области определения, поэтому точка x = 0 не является точкой экстремума этой функции.

Таким образом, условия о том, что производная функции в точке равна нулю или не существует, являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести и другие примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет. Поэтому нужно располагать достаточными признаками , позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно - максимум или минимум.

Теорема (первый достаточный признак существования экстремума функции). Критическая точка x 0 f (x ) , если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с "плюса" на "минус", то точкой максимума, а если с "минуса" на "плюс", то точкой минимума.

Если же вблизи точки x 0 , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки x 0 . В этом случае в точке x 0 экстремума нет.

Итак, чтобы определить точки экстремума функции, требуется выполнить следующее :

1. Найти производную функции.
2. Приравнять производную нулю и определить критические точки.
3. Мысленно или на бумаге отметить критические точки на числовой оси и определить знаки производной функции в полученных интервалах. Если знак производной меняется с "плюса" на "минус", то критическая точка является точкой максимума, а если с "минуса" на "плюс", то точкой минимума.
4. Вычислить значение функции в точках экстремума.

Пример 2. Найти экстремумы функции .

Решение. Найдём производную функции:

Приравняем производную нулю, чтобы найти критические точки:

.

Так как для любых значений "икса" знаменатель не равен нулю, то приравняем нулю числитель:

Получили одну критическую точку x = 3 . Определим знак производной в интервалах, разграниченных этой точкой:

в интервале от минус бесконечности до 3 - знак минус, то есть функция убывает,

в интервале от 3 до плюс бесконечности - знак плюс, то есть функция возрастает.

То есть, точка x = 3 является точкой минимума.

Найдём значение функции в точке минимума:

Таким образом, точка экстремума функции найдена: (3; 0) , причём она является точкой минимума.

Теорема (второй достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f (x ) , если вторая производная функции в этой точке не равна нулю (f ""(x ) ≠ 0 ), причём, если вторая производная больше нуля (f ""(x ) > 0 ), то точкой максимума, а если вторая производная меньше нуля (f ""(x ) < 0 ), то точкой минимума.

Замечание 1. Если в точке x 0 обращаются в нуль и первая, и вторая производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума функции.

Замечание 2. Второй достаточный признак экстремума функции неприменим и тогда, когда в стационарной точке первая производная не существует (тогда не существует и вторая производная). В этом случае также нужно вопользоваться первым достаточным признаком экстремума функции.

Локальный характер экстремумов функции

Из приведённых определений следует, что экстремум функции имеет локальный характер - это наибольшее и наименьшее значение функции по сравнению с близлежайшими значениями.

Предположим, вы рассматриваете свои заработки в отрезке времени протяжённостью в один год. Если в мае вы заработали 45 000 рублей, а в апреле 42 000 рублей и в июне 39 000 рублей, то майский заработок - максимум функции заработка по сравнению с близлежайшими значениями. Но в октябре вы заработали 71 000 рублей, в сентябре 75 000 рублей, а в ноябре 74 000 рублей, поэтому октябрьский заработок - минимум функции заработка по сравнению с близлежашими значениями. И вы легко видите, что максимум среди значений апреля-мая-июня меньше минимума сентября-октября-ноября.

Говоря обобщённо, на промежутке функция может иметь несколько экстремумов, причём может оказаться, что какой-либо минимум функции больше какого-либо максимума. Так, для функции изображённой на рисунке выше, .

То есть не следует думать, что максимум и минимум функции являются, соответственно, её наибольшим и наименьшим значениями на всём рассматриваемом отрезке. В точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума - наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума.

Поэтому можно уточнить приведённое выше понятие точек экстремума функции и называть точки минимума точками локального минимума, а точки максимума - точками локального максимума.

Ищем экстремумы функции вместе

Пример 3.

Решение.Функция определена и непрерывна на всей числовой прямой. Её производная существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых , т.е. , откуда и . Критическими точками и разбивают всю область определения функции на три интервала монотонности: . Выберем в каждой из них по одной контрольной точке и найдём знак производной в этой точке.

Для интервала контрольной точкой может служить : находим . Взяв в интервале точку , получим , а взяв в интервале точку , имеем . Итак, в интервалах и , а в интервале . Согласно первому достаточному признаку экстремума, в точке экстремума нет (так как производная сохраняет знак в интервале ), а в точке функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдём соответствующие значения функции: , а . В интервале функция убывает, так как в этом интервале , а в интервале возрастает, так как в этом интервале .

Чтобы уточнить построение графика, найдём точки пересечения его с осями координат. При получим уравнение , корни которого и , т. е. найдены две точки (0; 0) и (4; 0) графика функции. Используя все полученные сведения, строим график (см. в начале примера).

Пример 4. Найти экстремумы функции и построить её график.

Областью определения функции является вся числовая прямая, кроме точки , т.е. .

Для сокращения исследования можно воспользоваться тем, что данная функция чётная, так как . Поэтому её график симметричен относительно оси Oy и исследование можно выполнить только для интервала .

Находим производную и критические точки функции:

1) ;

2) ,

но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.

Таким образом, заданная функция имеет две критические точки: и . Учитывая чётность функции, проверим по второму достаточному признаку экстремума только точку . Для этого найдём вторую производную и определим её знак при : получим . Так как и , то является точкой минимума функции, при этом .

Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения:

(здесь символом обозначено стремление x к нулю справа, причём x остаётся положительным; аналогично означает стремление x к нулю слева, причём x остаётся отрицательным). Таким образом, если , то . Далее, находим

,

т.е. если , то .

Точек пересечения с осями график функции не имеет. Рисунок - в начале примера.

Продолжаем искать экстремумы функции вместе

Пример 8. Найти экстремумы функции .

Решение. Найдём область определения функции. Так как должно выполняться неравенство , то из получаем .

Найдём первую производную функции:

Найдём критические точки функции.

Обратимся к графику функции у = х 3 – 3х 2 . Рассмотрим окрестность точки х = 0, т.е. некоторый интервал, содержащий эту точку. Логично, что существует такая окрестность точки х = 0, что наибольшее значение функция у = х 3 – 3х 2 в этой окрестности принимает в точке х = 0. Например, на интервале (-1; 1) наибольшее значение, равное 0, функция принимает в точке х = 0. Точку х = 0 называют точкой максимума этой функции.

Аналогично, точка х = 2 называется точкой минимума функции х 3 – 3х 2 , так как в этой точке значение функции не больше ее значения в иной точке окрестности точки х = 2, например, окрестности (1,5; 2,5).

Таким образом, точкой максимума функции f(х) называется точка х 0 , если существует окрестность точки х 0 – такая, что выполняется неравенство f(х) ≤ f(х 0) для всех х из этой окрестности.

Например, точка х 0 = 0 – это точка максимума функции f(х) = 1 – х 2 , так как f(0) = 1 и верно неравенство f(х) ≤ 1 при всех значениях х.

Точкой минимума функции f(х) называется точка х 0 , если существует такая окрестность точки х 0 , что выполняется неравенство f(х) ≥ f(х 0) для всех х из этой окрестности.

Например, точка х 0 = 2 – это точка минимума функции f(х) = 3 + (х – 2) 2 , так как f(2) = 3 и f(х) ≥ 3 при всех х.

Точками экстремума называются точки минимума и точки максимума.

Обратимся к функции f(х), которая определена в некоторой окрестности точки х 0 и имеет в этой точке производную.

Если х 0 – точка экстремума дифференцируемой функции f(х), то f "(х 0) = 0. Это утверждение называют теоремой Ферма.

Теорема Ферма имеет наглядный геометрический смысл: в точке экстремума касательная параллельна оси абсцисс и поэтому ее угловой коэффициент
f "(х 0) равен нулю.

Например, функция f(х) = 1 – 3х 2 имеет в точке х 0 = 0 максимум, ее производная f "(х) = -2х, f "(0) = 0.

Функция f(х) = (х – 2) 2 + 3 имеет минимум в точке х 0 = 2, f "(х) = 2(х – 2), f "(2) = 0.

Отметим, что если f "(х 0) = 0, то этого недостаточно, чтобы утверждать, что х 0 – это обязательно точка экстремума функции f(х).

Например, если f(х) = х 3 , то f "(0) = 0. Однако точкой экстремума точка х = 0 не является, так как на всей числовой оси функция х 3 возрастает.

Итак, точки экстремума дифференцируемой функции необходимо искать лишь среди корней уравнения
f "(х) = 0, но корень этого уравнения не всегда является точкой экстремума.

Стационарными точками называют точки, в которых производная функции равна нулю.

Таким образом, для того, чтобы точка х 0 была точкой экстремума, необходимо, чтобы она была стационарной точкой.

Рассмотрим достаточные условия того, что стационарная точка является точкой экстремума, т.е. условия, при выполнении которых стационарная точка является точкой минимума или максимума функции.

Если производная левее стационарной точки положительна, а правее – отрицательна, т.е. производная меняет знак «+» на знак «–» при переходе через эту точку, то эта стационарная точка – это точка максимума.

Действительно, в данном случае левее стационарной точки функция возрастает, а правее – убывает, т.е. данная точка – это точка максимума.

Если производная меняет знак «–» на знак «+» при переходе через стационарную точку, то эта стационарная точка является точкой минимума.

Если производная знак не меняет при переходе через стационарную точку, т.е. слева и справа от стационарной точки производная положительна или отрицательна, то эта точка не является точкой экстремума.

Рассмотрим одну из задач. Найти точки экстремума функции f(х) = х 4 – 4х 3 .

Решение.

1) Найдем производную: f "(х) = 4х 3 – 12х 2 = 4х 2 (х – 3).

2) Найдем стационарные точки: 4х 2 (х – 3) = 0, х 1 = 0, х 2 = 3.

3) Методом интервалов устанавливаем, что производная f "(х) = 4х 2 (х – 3) положительна при х > 3, отрицательна при х < 0 и при 0 < х < 3.

4) Так как при переходе через точку х 1 = 0 знак производной не меняется, то эта точка не является точкой экстремума.

5) Производная меняет знак «–» на знак «+» при переходе через точку х 2 = 3. Поэтому х 2 = 3 – точка минимума.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Точка х 0 называетсяточкой максимума (минимума ) функцииf(х), если в некоторой окрестности точки х 0 выполняется неравенствоf(х) ≤f(х 0) (f(х) ≥f(х 0)).

Значение функции в этой точке называется соответственно максимумом илиминимумом функции. Максимум и минимум функции объединяются общим названиемэкстремума функции.

Экстремум функции в этом смысле часто называют локальным экстремумом , подчеркивая тот факт, что это понятие связано лишь с достаточно малой окрестностью точки х 0 . На одном и том же промежутке функция может иметь несколько локальных максимумов и минимумов, которые не обязательно совпадают сглобальным максимумом илиминимумом (т.е. наибольшим или наименьшим значением функции на всем промежутке).

Необходимое условие экстремума . Для того, чтобы функция имела экстремум в точке, необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Для дифференцируемых функций это условие вытекает из теоремы Ферма. Кроме того, оно предусматривает и случай, когда функция имеет экстремум в точке, в которой она не дифференцируема.

Точки, в которых выполнено необходимое условие экстремума, называются критическими (илистационарными для дифференцируемой функции). Эти точки должны входить в область определения функции.

Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая (необходимость условия). Заметим, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума, т.е. сформулированное условие не является достаточным.

Первое достаточное условие экстремума . Если при переходе через некоторую точку производная дифференцируемой функции меняет свой знак с плюса на минус, то это точка максимума функции, а если с минуса на плюс, - то точка минимума.

Доказательство этого условия вытекает из достаточного условия монотонности (при изменении знака производной происходит переход либо от возрастания функции к убыванию, либо от убывания к возрастанию).

Второе достаточное условие экстремума . Если первая производная дважды дифференцируемой функции в некоторой точке равна нулю, а вторая производная в этой точке положительна, то это точка минимума функции; а если вторая производная отрицательна, то это точка максимума.

Доказательство этого условия также основано на достаточном условии монотонности. В самом деле, если вторая производная положительна, то первая производная является возрастающей функцией. Поскольку в рассматриваемой точке она равна нулю, следовательно, при переходе через нее она меняет знак с минуса на плюс, что возвращает нас к первому достаточному условию локального минимума. Аналогично если вторая производная отрицательна, то первая убывает и меняет знак с плюса на минус, что является достаточным условием локального максимума.

Исследование функции на экстремум в соответствии со сформулированными теоремами включает следующие этапы:

1. Найти первую производную функции f`(x).

2. Проверить выполнение необходимого условия экстремума, т.е. найти критические точки функции f(x), в которых производнаяf`(x) = 0 или не существует.

3. Проверить выполнение достаточного условия экстремума, т.е. либо исследовать знак производной слева и справа от каждой критической точки, либо найти вторую производную f``(x) и определить ее знак в каждой критической точке. Сделать вывод о наличии экстремумов функции.

4. Найти экстремумы (экстремальные значения) функции.

Нахождение глобального максимума и минимума функции на некотором промежутке также имеет большое прикладное значение. Решение этой задачи на отрезке основано на теореме Вейерштрасса, в соответствии с которой непрерывная функция принимает на отрезке свои наибольшее и наименьшее значения. Они могут достигаться как в точках экстремума, так и на концах отрезка. Поэтому решение включает следующие этапы:

1. Найти производную функции f`(x).

2. Найти критические точки функции f(x), в которых производнаяf`(x) = 0 или не существует.

3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.

Что такое экстремум функции и каково необходимое условие экстремума?

Экстремумом функции называется максимум и минимум функции.

Необходимое условие максимума и минимума (экстремума) функции следующее: если функция f(x) имеет экстремум в точке х = а, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.

Это условие необходимое, но не достаточное. Производная в точке х = а может обращаться в нуль, в бесконечность или не существовать без того, чтобы функция имела экстремум в этой точке.

Каково достаточное условие экстремума функции (максимума или минимума)?

Первое условие:

Если в достаточной близости от точки х = а производная f?(x) положительна слева от а и отрицательна справа от а, то в самой точке х = а функция f(x) имеет максимум

Если в достаточной близости от точки х = а производная f?(x) отрицательна слева от а и положительна справа от а, то в самой точке х = а функция f(x) имеет минимум при условии, что функция f(x) здесь непрерывна.

Вместо этого можно воспользоваться вторым достаточным условием экстремума функции:

Пусть в точке х = а первая производная f?(x) обращается в нуль; если при этом вторая производная f??(а) отрицательна, то функция f(x) имеет в точке x = a максимум, если положительна - то минимум.

Что такое критическая точка функции и как её найти?

Это значение аргумента функции, при котором функция имеет экстремум (т.е. максимум или минимум). Чтобы его найти, нужно найти производную функции f?(x) и, приравняв её к нулю, решить уравнение f?(x) = 0. Корни этого уравнения, а также те точки, в которых не существует производная данной функции, являются критическими точками, т. е. значениями аргумента, при которых может быть экстремум. Их можно легко определить, взглянув на график производной : нас интересуют те значения аргумента, при которых график функции пересекает ось абсцисс (ось Ох) и те, при которых график терпит разрывы.

Для примера найдём экстремум параболы .

Функция y(x) = 3x2 + 2x - 50.

Производная функции: y?(x) = 6x + 2

Решаем уравнение: y?(x) = 0

6х + 2 = 0, 6х = -2, х=-2/6 = -1/3

В данном случае критическая точка - это х0=-1/3. Именно при этом значении аргумента функция имеет экстремум . Чтобы его найти , подставляем в выражение для функции вместо «х» найдённое число:

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Как определить максимум и минимум функции, т.е. её наибольшее и наименьшее значения?

Если знак производной при переходе через критическую точку х0 меняется с «плюса» на «минус», то х0 есть точка максимума ; если же знак производной меняется с минуса на плюс, то х0 есть точка минимума ; если знак не меняется, то в точке х0 ни максимума, ни минимума нет.

Для рассмотренного примера:

Берём произвольное значение аргумента слева от критической точки: х = -1

При х = -1 значение производной будет у?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (т.е. знак - «минус»).

Теперь берём произвольное значение аргумента справа от критической точки: х = 1

При х = 1 значение производной будет у(1) = 6*1 + 2 = 6 + 2 = 8 (т.е. знак - «плюс»).

Как видим, производная при переходе через критическую точку поменяла знак с минуса на плюс. Значит, при критическом значении х0 мы имеем точку минимума.

Наибольшее и наименьшее значение функции на интервале (на отрезке) находят по такой же процедуре, только с учетом того, что, возможно, не все критические точки будут лежать внутри указанного интервала. Те критические точки, которые находятся за пределом интервала, нужно исключить из рассмотрения. Если внутри интервала находится только одна критическая точка - в ней будет либо максимум, либо минимум. В этом случае для определения наибольшего и наименьшего значений функции учитываем также значения функции на концах интервала.

Например, найдём наибольшее и наименьшее значения функции

y(x) = 3sin(x) — 0,5х

на интервалах:

Итак, производная функции —

y?(x) = 3cos(x) — 0,5

Решаем уравнение 3cos(x) — 0,5 = 0

cos(x) = 0,5/3 = 0,16667

х = ±arccos(0,16667) + 2πk.

Находим критические точки на интервале [-9; 9]:

х = arccos(0,16667) — 2π*2 = -11,163 (не входит в интервал)

х = -arccos(0,16667) — 2π*1 = -7,687

х = arccos(0,16667) — 2π*1 = -4,88

х = -arccos(0,16667) + 2π*0 = -1,403

х = arccos(0,16667) + 2π*0 = 1,403

х = -arccos(0,16667) + 2π*1 = 4,88

х = arccos(0,16667) + 2π*1 = 7,687

х = -arccos(0,16667) + 2π*2 = 11,163 (не входит в интервал)

Находим значения функции при критических значениях аргумента:

y(-7,687) = 3cos(-7,687) — 0,5 = 0,885

y(-4,88) = 3cos(-4,88) — 0,5 = 5,398

y(-1,403) = 3cos(-1,403) — 0,5 = -2,256

y(1,403) = 3cos(1,403) — 0,5 = 2,256

y(4,88) = 3cos(4,88) — 0,5 = -5,398

y(7,687) = 3cos(7,687) — 0,5 = -0,885

Видно, что на интервале [-9; 9] наибольшее значение функция имеет при x = -4,88:

x = -4,88, у = 5,398,

а наименьшее - при х = 4,88:

x = 4,88, у = -5,398.

На интервале [-6; -3] мы имеем только одну критическую точку: х = -4,88. Значение функции при х = -4,88 равно у = 5,398.

Находим значение функции на концах интервала:

y(-6) = 3cos(-6) — 0,5 = 3,838

y(-3) = 3cos(-3) — 0,5 = 1,077

На интервале [-6; -3] имеем наибольшее значение функции

у = 5,398 при x = -4,88

наименьшее значение —

у = 1,077 при x = -3

Как найти точки перегиба графика функции и определить стороны выпуклости и вогнутости?

Чтобы найти все точки перегиба линии y = f(x), надо найти вторую производную, приравнять её к нулю (решить уравнение) и испытать все те значения х, для которых вторая производная равна нулю, бесконечна или не существует. Если при переходе через одно из этих значений вторая производная меняет знак, то график функции имеет в этой точке перегиб. Если же не меняет, то перегиба нет.

Корни уравнения f ? (x) = 0, а также возможные точки разрыва функции и второй производной разбивают область определения функции на ряд интервалов. Выпуклость на каждом их интервалов определяется знаком второй производной. Если вторая производная в точке на исследуемом интервале положительна, то линия y = f(x) обращена здесь вогнутостью кверху, а если отрицательна - то книзу.

Как найти экстремумы функции двух переменных?

Чтобы найти экстремумы функции f(x,y), дифференцируемой в области её задания, нужно:

1) найти критические точки, а для этого — решить систему уравнений

fх? (x,y) = 0, fу? (x,y) = 0

2) для каждой критической точки Р0(a;b) исследовать, остается ли неизменным знак разности

для всех точек (х;у), достаточно близких к Р0. Если разность сохраняет положительный знак, то в точке Р0 имеем минимум, если отрицательный - то максимум. Если разность не сохраняет знака, то в точке Р0 экстремума нет.

Аналогично определяют экстремумы функции при большем числе аргументов.

Какой официальный сайт певицы Мики Ньютон и её группы
Новое украинское чудо - Мика Ньютон! Это группа из 5 человек, играющая поп-рок, наслаждающаяся жизнью, дарящая драйв и позитивно смотрящая на эту жизнь. Собрались ребята в Киеве, где в настоящий момент и обитают. Ребята ни в какую не соглашаются со стандартными устоями в музыке и жизни, открывая своё новое звучание и ломая всевозможные стандарты. Лидер коллектива -

Как перевести миллилитры в кубические метры
Основной единицей длины в системе СИ является метр. Исходя из этого, основной единицей объёма следует считать кубический метр, или, как его ещё называют, кубометр или куб. Это — объём куба с ребрами, равными одному метру. Однако, на практике выражать объём именно в кубометрах удобно не всегда. Например, объём комнаты в кубических метрах выражать удобно: умножили длину ко

Какая калорийность манной крупы
Калорийность продуктов питания, таблица калорийности. Потребность человека в энергии измеряется в килокалориях (ккал). Слово «калория» пришло из латинского языка и означает «тепло». В физике калориями измеряется энергия. Одна килокалория - это такое количество энергии,

Какие есть этапы развития реализма в литературе
Реализм (лат. вещественный, действительный) — направление в литературе и искусстве, ставящее целью правдивое воспроизведение действительности в её типических чертах. Общие признаки: Художественное изображение жизни в образах, соответствующее сути явлений самой жизни. Реальность является средством познания человеком себя и окружающего мира. Типизация

Какова связь между берклием и 117-м элементом таблицы Менделеева
Берклий, Berkelium, Bk — 97-й элемент таблицы Менделеева.Открыт в декабре 1949 г. Томпсоном, Гиорсо и Сиборгом в Калифорнийском университете в Беркли. При облучении 241Am альфа-частицами они получили изотоп беркелия 243Вk. Поскольку Bk обладает структурным сходством с тербием, получившим свое название от имени г. Иттерби в

Чем прославился Ярослав Мудрый
Ярослав Мудрый (980-1054), великий князь киевский (1019). Сын Владимира I Святославовича. Изгнал Святополка I Окаянного, боролся с братом Мстиславом, разделил с ним государство (1025), в 1035 г. вновь объединил его. Рядом побед обезопасил южные и западные границы Руси. Установил династические связи с многими странами Ев

Как появилась традиция кричать на свадьбе "Горько!"
Давным-давно появилась традиция кричать во время свадебного застолья: «Горько!», вынуждая молодоженов встать со своих мест и поцеловаться. Сегодня многие даже не догадываются, в чем же заключается смысл этого обряда.В старину на свадьбах кричали «Горько!», давая понять, что вино в чашах якобы несладкое. А

Каковы симптомы ларингита
Ларингит (от др.-греч. λ?ρυγξ — гортань) — воспаление гортани, связанное, как правило, с простудным заболеванием либо с такими инфекционными заболеваниями, как корь, скарлатина, коклюш. Развитию заболевания способствуют переохлаждение, дыхание через рот, запылённый

Определяется ли род и склонение у существительных, имеющих только форму множественного числа
Число — это грамматическая категория, выражающая количественную характеристику предмета. 1. Большинство имён существительных изменяется по числам, т.е. имеет две формы — единственного и множественного числа. В форме единственного числа существительное обозначает один предмет, в форме множественного числа — несколько предметов:

Чем полезна русская каша
Гречневая каша Гречка - крупа особенная. Из нее, получается, пожалуй, одна из самых полезных каш. Недаром мы называем ее первой. Гречка содержит клетчатку, целый спектр витаминов — Е, РР, В1, В2, фолиевые и органические кислоты, а так же большой процент крахмала, способствующего попаданию в организм нужного количества нео

Интерактивную карту города Архангельска можно посмотреть на следующих сайтах: Карта1 - спутниковая и стандартная карта;Карта2 - стандартная карта (1:350 000); Карта3 - есть названия улиц, номера домов, возможен поиск по улице;Карта4 - карта с названиями улицКарта5 - интерактивная карта города;Карта6 - интерактивная карта города.