Уравнение f x 1. Уравнения, допускающие понижение порядка. Уравнение касательной и уравнение нормали к графику функции

1. Преобразовать заданное уравнение к виду F(x) = 0.

2. Построить таблицу значений функции на заданном отрезке.

3. Построить график функции F(x).

4. Локализовать корни, т. е. найти интервалы, на которых корни уравнения существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположные знаки.

5. Определить по графику первый из корней уравнения и первый отрезок локализации этого корня.

6. Методом половинного деления найти корень уравнения с точностью e=0,001.

7. Повторить пункты 5 и 6 для следующих корней уравнения.

Вариант уравнения выбирается по номеру студента в списке.

Варианты уравнений

1. Найти корни нелинейного алгебраического уравнения

2. Найти корни нелинейного алгебраического уравнения

на отрезке .

3. Найти корни нелинейного алгебраического уравнения

при .

4. Решить нелинейное уравнение

на отрезке .

5. Решить нелинейное уравнение

и найти его корни на отрезке .

6. Найти корни нелинейного алгебраического уравнения

Поэтому возникает естественное желание свести уравнение порядка выше первого к уравнению более низкого порядка. В некоторых случаях это удаётся сделать. Рассмотрим их.

1. Уравнения вида y (n) =f(x) решаются последовательным интегрированием n раз
, ,… .
Пример . Решить уравнение xy""=1 . Можем записать , следовательно, y"=ln|x| + C 1 и, интегрируя ещё раз, окончательно получаем y=∫ln|x| + C 1 x + C 2

2. В уравнениях вида F(x,y (k) ,y (k +1) ,..,y (n))=0 (то есть не содержащих в явном виде неизвестной функции и некоторых её производных) порядок понижается с помощью замены переменной y (k) = z(x). Тогда y (k +1) =z"(x),…,y (n) = z (n - k) (x) и мы получаем уравнение F(x,z,z",..,z (n - k)) порядка n-k. Его решением является функция z = φ(x,C 1 ,C 2 ,…,C n) или, вспоминая, что такое z, получаем уравнение y (n- k) = φ(x,C 1 ,C 2 ,…,C n - k) рассмотренного в случае 1 типа.
Пример 1 . Решить уравнение x 2 y"" = (y") 2 . Делаем замену y"=z(x) . Тогда y""=z"(x) . Подставляя в исходное уравнение, получаем x 2 z"=z 2 . Разделяя переменные, получаем . Интегрируя, имеем , или, что тоже самое, . Последнее соотношение записывается в виде , откуда . Интегрируя, окончательно получаем
Пример 2 . Решить уравнение x 3 y"" +x 2 y"=1 .Делаем замену переменных: y"=z; y""=z"
x 3 z"+x 2 z=1. Делаем замену переменных: z=u/x; z"=(u"x-u)/x 2
x 3 (u"x-u)/x 2 +x 2 u/x=1 или u"x 2 -xu+xu=1 или u"x^2=1. Откуда: u"=1/x 2 или du/dx=1/x 2 или u = int(dx/x 2) = -1/x+c 1
Поскольку z=u/x, то z = -1/x 2 +c 1 /x. Поскольку y"=z, то dy/dx=-1/x 2 +c 1 /x
y = int(c 1 dx/x-dx/x 2) =c 1 ln(x) + 1/x + c 2 . Ответ: y = c 1 ln(x) + 1/x + c 2

3. Следующим уравнением, допускающим понижение порядка, является уравнение вида F(y,y",y"",…,y (n))=0 , не содержащее в явном виде независимой переменной. Порядок уравнения понижается с помощью замены переменной y"=p(y) , где p - новая искомая функция, зависящая от y. Тогда
= и так далее. По индукции имеем y (n) =φ(p,p",..,p (n-1)). Подставляя в исходное уравнение, понижаем его порядок на единицу.

Пример . Решить уравнение (y") 2 +2yy""=0 . Делаем стандартную замену y"=p(y) , тогда y″=p′·p . Подставляя в уравнение, получаем Разделяя переменные, при p≠0, имеем Интегрируя, получаем или, что то же самое, . Тогда или . Интегрируя последнее равенство, окончательно получаем При разделении переменных мы могли потерять решение y=C, которое получается при p=0, или, что то же самое, при y"=0, но оно содержится в полученном выше.

4. Иногда удаётся подметить особенность, позволяющую понизить порядок уравнения отличными от рассмотренных выше способами. Покажем это на примерах.

Примеры .
1. Если обе части уравнения yy"""=y′y″ разделить на yy″, то получим уравнение , которое можно переписать в виде (lny″)′=(lny)′. Из последнего соотношения следует, что lny″=lny+lnC , или, что то же самое, y″=Cy . Получилось уравнение на порядок ниже и рассмотренного ранее типа.
2. Аналогично для уравнения yy″=y′(y′+1) имеем , или (ln(y"+1))" = (lny)" . Из последнего соотношения следует, что ln(y"+1) = lny + lnC 1 , или y"=C 1 y-1. Разделяя переменные и интегрируя, получаем, ln(C 1 y-1) = C 1 x+C 2
Решить уравнения, допускающие понижение порядка можно с помощью специального сервиса

2.2 Методика решения уравнений и неравенств

Уравнения и неравенства традиционная тема школьного курса математики, занимающая большое место, начиная с младших классов, где простейшие уравнения и неравенства до введения теории на основе свойств арифметических действий, и кончая старшими классами, где решаются трансцендентные уравнения.

Уравнения и неравенства представляют собой тот алгебраический аппарат, тот язык, на который переводятся разного рода задачи, в том числе и прикладные, строятся их математические модели.

Использование монотонности функций при решении уравнений и неравенств. Одну из наиболее часто встречающихся идей хорошо иллюстрирует решение следующего простого неравенства:

1. Решить неравенство: .

Решение. Есть два стандартных пути решения: возведение в квадрат (при условии
; если же
, неравенство выполняется) и замена неизвестного
.

Рассмотрим еще один способ – нестандартный. Функция, расположенная в левой части, монотонно возрастает, в первой части убывает. Из очевидных графических соображений следует, что уравнение
x 0 – решение этого уравнения, то при
будет, а решением данного неравенства будет
. Значение x 0 легко подбирается: x 0 = 1.

Ответ .
.

2. Решить уравнение:
.

Решение. Данное уравнение имеет очевидное решение x = 1. Докажем, что других решений нет. Поделим обе части на , получим
. Левая часть представляет собой монотонно убывающую функцию. Следовательно, каждое свое значение она принимает один раз, т.е. данное уравнение имеет единственное решение.

Ответ . x = 1.

Итак, основная идея, на которой основывались решения этих двух примеров, весьма проста: если f (x ) монотонно возрастает, а φ (x) монотонно убывает, то уравнение f (x ) = φ (x ) имеет не более одного решения, причем если x = x 0 – решение этого уравнения, то при x > x 0 (x входит в область определения обеих функций f (x ) и φ (x ) ) будет f (x ) > φ (x ) , а при x x 0 будет

f (x ) φ (x ) .

Стоит обратить внимание на одну модификацию этой идеи, а именно: если f (x ) – монотонная функция, то из равенства f (x ) = f (y ) следует, что x = y .

3. Решить уравнение: .

Решение. Преобразуем уравнение:

.

Рассмотрим функцию
.

Докажем, что при t > 1 эта функция монотонно убывает. Это можно сделать, например, стандартным образом: найти производную

и доказать, что при t > 1
. Покажем другой способ:

.

Получившаяся функция, очевидно, является убывающей (основание растет, под знаком логарифма функция убывает).

Наше уравнение имеет вид: , значит,
. Слева функция возрастающая, следовательно, решение единственно, оно легко находится подбором: x = 4.

Ответ . x = 4 .

Уравнения вида f ( f ( x )) = x . При решении уравнений указанного вида полезна бывает теорема:

Если y = f(x) – монотонно возрастающая функция, то уравнения

f (x ) = x (А)

f (f (x )) = x (Б)

эквивалентны .

Доказательство. То, что уравнение (Б) является следствием уравнения (А), очевидно: любой корень (А) удовлетворяет (Б). (Если

f (x 0 ) = x 0 , то f (f (x 0 )) = f (x 0 ) = x 0 .). Докажем, что любой корень уравнения (Б) удовлетворяет уравнению (А). Пусть x 0 такое, что f (f (x 0 )) = x 0 .Предположим, что f (x 0 ) ≠ x 0 и для определенности f (x 0 ) > x 0 . Тогда f (f (x 0 )) > f (x 0 ) > x 0 , что противоречит предположению ( f (f (x 0 )) = x 0). Теорема доказана.

Верна ли теорема для монотонно убывающей функции?

Замечание. Если y = f (x ) монотонно возрастает, то при любом k уравнения
и f (x ) = x эквивалентны.

Приведем несколько примеров использования этой теоремы .

1. Решить уравнение:
.

Решени е. Перепишем уравнение
. Рассмотрим функцию
. Эта функция монотонно возрастает. Имеем уравнение

f (f (x )) = x . В соответствии с теоремой заменяем его на эквивалентное уравнение f (x ) = x или .

Ответ.

.

2. Решить уравнение:

.

Решение. Преобразуем уравнение:
.

Данное уравнение имеет вид: f (f (x )) = x , где
.

Согласно теореме имеем эквивалентное уравнение:
,

Ответ.
.

3. Решить систему уравнений :
.

Решение. Рассмотрим функцию. Поскольку

При всех t , то f (t ) возрастает.

Система имеет вид y = f (x ), z = f (y ), x = f (z ), т.е. x = f (f (f (x ))).

Согласно теореме x удовлетворяет уравнению f (x ) = x или

Ответ. (0, 0, 0), (-1, -1, -1).

Использование экстремальных свойств рассматриваемых функций. Оценки. Основные идеи этого пункта достаточно хорошо видны из примеров:

1. Решить уравнение:
.

Решение. Левая часть данного уравнения не превосходит 2, а правая- не меньше 2. Следовательно, равенство может иметь место лишь при условии, что левая и правая части равны 2, т.е. x = 0.

Замечание. Данная ситуация, когда наименьшее значение функции, расположенной в одной части уравнения, равно наибольшему значению функции, расположенной в другой части, может быть обобщена. Более общий случай – уравнения вида f (x ) = φ (x ) , для которых
при всех допустимых x (формально мы можем переписать это уравнение в виде

f (x ) = φ (x ) = 0, в результате приходим к уже рассмотренной ситуации, поскольку наибольшее значение правой части равно нулю).

2. Решить уравнение: .

Докажем, что данное уравнение не имеет решений. Перейдем к следствию (потенцируем):
.

Оценим левую часть на основании неравенства между средним геометрическим и средним арифметическим

:

т.е. левая часть меньше правой. Уравнение не имеет решений.

Ответ. Нет решения.

3. Решить систему уравнений:

Решение. Докажем, что.

Пусть для определенности x 5 > x 4 , тогда из первых двух уравнений получим , откуда
и тем более
. Далее из третьего и четвертого получаем
и тем более
. Из последней пары находим
. Получилось противоречие ( и
, т.е.
, а предположили, что ).

Значит,
, отсюда
и т.д., все неизвестные равны между собой.

Ответ. (0, 0, 0, 0,0);
.

Нестандартные по формулировке задачи, связанные с уравнениями или неравенствами. К данной категории, в частности, относятся задачи, в которых требуется определить число корней заданного уравнения, доказать существование корня на определенном промежутке, решить уравнение или неравенство на заданном промежутке. Рассмотрим несколько примеров.

1. Доказать, что уравнение
имеет одно положительное решение и одно отрицательное решение. методике преподавания математики в средней школе : Учеб. пособие для студентов...

Обучение аудированию с опорой на видеоматериалы в старших классах средней школы

Дипломная работа >> Педагогика

... старших классах средней школы . Глава 2 посвящена особенностям методики обучения аудированию на старшем ... умственной деятельности, повышению интереса к работе... задача весьма сложная. Для решения этой задачи ... задача подготовительного этапа - снять трудности ...

Методы решения уравнений содержащих параметр

Дипломная работа >> Математика

Изучения методов решения уравнений, содержащих параметры, в старших классах средней школы и в разработке соответствующей методики . Решение этой проблемы... задача повышенной трудности . При повторении курса алгебры и начала анализа 10 класса в системе задач ...

Школа и общественное дошкольное воспитание в период восстановления и дальнейшего развития народного хозяйства СССР (1946-1958 гг.)

Конспект >> Педагогика

Учащихся старших классов средней школы . Если... классов средней школы . На протяжении более двух десятилетий училищам приходилось решать одновременно две задачи ... раскрывали методику руководства ими... решения поставили вопрос о повышении ... нарастания трудности и...

Методика использования эвристического метода

Реферат >> Социология

... методике использования эвристического метода преподавания материала по логарифмической функции в 11 классе средней школы ... обучающийся в старшем классе средней школы , уже включен... навыки: - решение задач на логарифмы + + - решение задач повышенной трудности + - ...

Пусть дано уравнение f(x) = 0 . Число x называется корнем данного уравнения, если оно, будучи подставленным в уравнение, обращает его в равенство, то есть f(x) = 0 . Число x называют нулем функции f(x) .Нахождение корней уравнения с определенной точностью можно разделить на два этапа:

1) отделение корней, то есть установление промежутков, в которых содержится один корень уравнения;

2) вычисление корня, принадлежащего выбранному промежутку, с заданной точностью.

Известно, что если функция f(x) непрерывна и принимает на концах отрезка [a, b ] значения разных знаков, то есть f(a)× f(b) < 0 , то внутри этого отрезка найдется нуль функции.

Для отделения (или локализации) корня уравнения f(x) = 0 для непрерывной в области определения функции f(x) можно составить таблицу значений функции у = f(x) на определенном промежутке изменения аргумента х . Если для некоторых соседних значений аргумента значения функции имеют разные знаки, то нуль функции находится между ними.

Пусть дано уравнение f(x) = 0 , где функция f(x) непрерывна на отрезке [a, b ] и f(a)× f(b) < 0 .Для вычислениякорня данного уравнения
x Î [a, b ] находится середина этого отрезка x 1 = 0,5(a+b) . Если f(x 1) ¹ 0 , то для продолжения вычислений выбирается та из частей данного отрезка
[a, х 1 ] или [х 1 , b ] , на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначаются а 1 и b 1 . Новый отрезок [a 1 , b 1 ] снова делится пополам и производятся вычисления по изложенной схеме и так далее. В результате получается либо точный корень заданного уравнения на каком-то этапе, либо последовательность вложенных отрезков [a, b ] ,
[a 1 , b 1 ] , … , [a n , b n ] , …, таких что:

f(a n)× f(b n) < 0 , n =1, 2, …

Число x - общий предел последовательностей (а n) и (b n) – является корнем уравнения f(x) = 0 .

Оценка погрешности решения на n -ом шаге вычислений имеет вид.

Касательная - это прямая , которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой .

Выведем уравнение касательной, а затем - уравнение нормали к графику функции.

y = kx + b .

В нём k - угловой коэффициент.

Отсюда получаем следующую запись:

y - y 0 = k (x - x 0 ) .

Значение производной f "(x 0 ) функции y = f (x ) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f (x 0 ) . В этом состоит геометрический смысл производной .

Таким образом, можем заменить k на f "(x 0 ) и получить следующее уравнение касательной к графику функции :

y - y 0 = f "(x 0 )(x - x 0 ) .

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде . Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль - это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет "холодным душем".

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Найдём производную функции:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример - тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг - приведение уравнения к общему виду.

Пример 2.

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в "формулу-болванку" и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

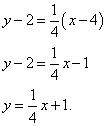
Перед тем, как привести уравнение к общему виду, нужно его немного "причесать": умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали - не заметить, что функция, данная в примере, - сложная и вычислять её производную как производную простой функции. Следующие примеры - уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция - сложная, так как аргумент тангенса (2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции.